Précis de thermodynamique
|
|
|
- Marc Milot
- il y a 10 ans
- Total affichages :
Transcription
1 M. Hubert N. Vandewalle Précis de thermodynamique Année académique PHYS Thermodynamique
2 2 Ce précis a été créé dans le but d offrir à l étudiant une base solide pour l apprentissage de la thermodynamique. Il trouvera dans chaque chapitre un court rappel théorique où l essentiel de la matière est présentée. Chaque chapitre propose aussi quelques exercices qui couvrent la matière abordée. Sont traitées, en premier lieu, les diverse notions mathématiques nécessaires au cours théorique : différentielles exacte et inexacte, opérateur de dérivation vectoriel, développement en série et transformation de Legendre. S en suis, au second chapitre, les concepts de dilatation thermique et d échange de chaleur. Le troisième chapitre traite des diverses transformations que peuvent subir un gaz, des machines thermiques et de la variation d entropie lors des transformations. Le quatrième chapitre donne quelques bases de physique statistique pour offrir à l étudiant une intuition de la notion d entropie. Le cinquième chapitre décrit les divers potentiels existant en thermodynamique et ainsi que leurs utilités, l étude des équilibres thermodynamiques est aussi présentée. Finalement, le dernier chapitre étudie les mélange et les transitions de phase. Les exercices proposés dans ce précis ont pour but d aider à la compréhension du cours théorique par l application et l illustration. Certains d entre eux seront étudiés et résolus lors des séances de travaux pratiques. Il est cependant important pour l étudiant de comprendre que les exercices non-résolus en cours théoriques ou lors des travaux pratiques lui sont laissés à titre d entraînement. Toute la matière étudiée et reprise dans ce recueil est susceptible d être le sujet de questions lors de l examen final. Maxime Hubert, septembre Contacts Maxime Hubert Bureau : B5a, 3 e étage, bureau 3/56, Téléphone : [email protected] Nicolas Vandewalle Bureau : B5a, 3 e étage, bureau 3/54, Téléphone : [email protected]
3 Table des matières 1 Outils mathématiques Rappels Dérivée d une fonction d une seule variable Dérivée d une fonction de plusieurs variables Opérateur de dérivation Nabla Gradient d un champ scalaire Divergence d un champ vectoriel Rotationnel d un champ vectoriel Laplacien d un champ scalaire Dérivées secondes Développement en série de Taylor Différentielles inexactes Transformation de Legendre Exercices Calorimétrie & Dilatation Rappels Calorimétrie Dilatation Exercices Transformations & Machines thermiques Rappels Transformations d une gaz Transformations isobares Transformations isochores Transformations isothermes Transformations adiabatiques Machines thermiques Cycles moteurs Cycles récepteurs Exercices Elements de physique statistique Rappels Éléments de statistique et probabilité L entropie de Boltzmann Exercices Potentiels et équilibres thermodynamiques Rappels Différentielle exacte de l énergie interne et équations d état Transformation de Legendre et potentiels thermodynamiques Énergie libre F Enthalpie G Enthalpie libre H Grand potentiel J Équilibres thermodynamiques Exercices
4 4 TABLE DES MATIÈRES 6 Mélanges et changements de phase Rappels Mélanges Changements de phase Relation de Clapeyron Point critique Exercices
5 Séance 1 Outils mathématiques 1.1 Rappels Dérivée d une fonction d une seule variable Soit une fonction d une seule variable f : R R : x f(x). Sa dérivée au point x = x 0 est définie comme df dx x=x0 = lim x 0 f(x 0 + x) f(x 0 ), (1.1) x et représente la tangente à f(x) au point x = x 0. Cette définition est illustrée à la figure 1.1. Une autre approche peut-être utilisée afin de décrire la dérivée d une fonction : au point x 0, alors que l argument x varie d une quantité x, l image f(x) varie d une quantité f. Nous pouvons donc relier la variation f à la variation x, dans le cas où x est faible, comme f a x, (1.2) où a est un coefficient de proportionnalité à définir. Géométriquement, depuis la figure 1.1, nous pouvons constater que le coefficient a n est autre, au point x = x 0, que la dérivée de la fonction f en x = x 0. Ainsi, f df x. (1.3) dx x=x0 Ce résultat s interprète comme suit : Près de x 0, lorsque x est faible, la fonction f(x), peut être vue comme une droite. Dès lors, la valeur de f(x 0 + x) est approchée par f(x 0 + x) f(x 0 ) + x df. (1.4) dx x=x0 Traditionnellement, quand la variation x est faible, nous la notons dx. Ainsi, l équation (1.3) s écrit, dans ces notations, comme df = a dx (1.5) () ( +Δ) ( ) +Δ Figure 1.1 Dérivée d une fonction f(x) en un point x 0 et approche géométrique de la notion de différentielle d une fonction. 5
6 6 SÉANCE 1. OUTILS MATHÉMATIQUES Il s agit de la différentielle de la fonction f par rapport à la variable x où a = df/dx x=x0 exprimant la variation infinitésimale df en fonction de dx au point x Dérivée d une fonction de plusieurs variables Considérons maintenant une fonction f de deux variables, définie comme f : R 2 R : (x, y) f(x, y). Dans le cadre d une fonction de deux variables, nous définissons les dérivées partielles de f par rapport à x et y au point (x 0, y 0 ) comme suit f x f y x=x0,y=y 0 x=x0,y=y 0 = lim x 0 = lim y 0 f(x 0 + x, y 0 ) f(x 0, y 0 ), x (1.6) f(x 0, y 0 + y) f(x 0, y 0 ). y (1.7) Ces définitions s interprètent comme suit : la dérivée f/ x correspond à la variation de f(x, y) le long de l axe x tout en laissant la valeur de y constante. Il s agit donc de la même définition que dans la section précédente, où y est laissé invariant. Ainsi, nous dérivons partiellement la fonction f le long de l axe x, rien n est considéré selon l axe y. La dérivée f/ y est identique si ce n est que y supplante x dans la raisonnement précédent. Ces définitions présentent cependant un inconvénient car, comme leur nom l indique, ces dérivées ne sont que partielles. Nous n avons pas, simultanément, une information sur la variation selon x et selon y. Afin de se soustraire de ce problème, tentons une approche différentielle, c est-à-dire, d obtenir une expression de la forme df = a dx + b dy, (1.8) où les variations dx, dy et df sont supposées petites. Dans la continuité du raisonnement proposé dans la section précédente, nous pouvons comprendre que a mesure la variation de la fonction f lorsque change la valeur de x seulement (y est maintenue fixe). De manière similaire, b mesure la variation de f conséquente aux changements de y seulement (x est maintenue fixe). Le coefficient a (resp. b) représente donc le coefficient de proportionnalité de la croissance de f par rapport à x (resp. y), ce que mesure la dérivée partielle f/ x (resp. f/ y). Ainsi, la différentielle (1.8) s exprime df = f dx + f dy. (1.9) x y y x A cette étape, nous pouvons légitimement nous interroger sur le lien que possède la notion de différentielle avec les notions déjà connues de dérivation de fonctions de plusieurs variables. Pour répondre à cette question, supposons que les variables x et y possède une dépendance temporelle explicite, c est-a-dire que nous pouvons écrire x(t) et y(t). Ainsi, la fonction f dépend implicitement du temps t et nous pouvons calculer la dérivée de f par rapport au temps. Le théorème de dérivation de fonctions implicites nous permet d écrire df dt = f dx x y dt + f dy y x dt. (1.10) Si nous comparons l équation (1.10) avec l équation (1.9), nous constatons que la dérivation par rapport au temps n a eu d effet que sur les facteurs dx et dy, les pré-facteurs f/ x et f/ y restant inchangés. De manière un peu imagée, nous pouvons voir la différentielle de l équation (1.9) comme une forme pré-dérivée de la fonction f. En effet, nous ne dérivons totalement la fonction f qu à l équation (1.10). D où le nom de cette forme, la dérivée totale de f par rapport à t. Nos considérations sur les fonctions à deux variables s étendent facilement à n dimensions. Les n dérivées partielles de la fonction f autour du point (x 1,0,..., x n,0 ) sont données par les n égalités f f(x 1,0,..., x i,0 + x i,..., x n,0 ) f(x 1,0,..., x i,0,..., x n,0 ) = lim, (1.11) x i xj,i j x i 0 x i où i {1,..., n}. La différentielle de la fonction f de n variables est alors df = f dx x 1 x2,...,x f dx n n x n x1,...,x n 1 (1.12) n f = dx i. x i xj,i j (1.13) i=1 Finalement, la dérivée totale, dans le cas d une dépendance temporelle implicite, est
7 1.1. RAPPELS 7 df dt = f dx 1 x 1 x2,...,x n dt + + f dx n x n x1,...,x n 1 dt, (1.14) n f dx i = x i xj,i j dt. (1.15) i= Opérateur de dérivation Nabla Dans cette section, nous travaillerons dans l espace tri-dimensionnel R 3. Dans ce cadre, l opérateur vectoriel de dérivation Nabla, s écrit de manière symbolique sous la forme = (.,.,. ). (1.16) x y,z y x,z z x,y Il s agit du vecteur contenant les dérivées par rapport à chaque variable de l espace R 3. Gradient d un champ scalaire Soit un champ scalaire f : R 3 R : (x, y, z) f(x, y, z). Le gradient du champ f est f = ( f, f, f ), (1.17) x y,z y x,z z x,y résultat de l application de l opérateur nabla sur le champs scalaire f. La propriété fondamentale du gradient est d indiquer, en chaque point, le sens des plus grandes croissances du champ scalaire considéré. Prenons l exemple de la température dans uns pièce. La température définit un champ scalaire T (x, y, z) en chaque point de la pièce. Dans ce cas, le gradient nous indique la direction des zones les plus chaudes en chaque point. Une autre propriété à retenir est le lien entre f et la dérivée totale introduite précédemment. En effet, supposons que nous nous déplacions dans un champ scalaire, la température dans un pièce pour reprendre l exemple précédent. Nos coordonnées (x, y, z) seraient alors variables dans le temps. Dès lors, nous ressentirions dans l espace une température différente à chaque instant, conséquence de notre déplacement. Le calcul de la dérivée totale nous donne df dt = f dx x y,z dt + f dy y x,z dt + f dz z x,y dt, (1.18) = v. f. (1.19) Ainsi, la dérivée totale du champ scalaire f nous est donnée par la projection de la vitesse v sur le gradient f. En conséquence, une dérivée totale nulle correspond à un mouvement dans l espace toujours perpendiculaire aux plus fortes croissances du champ. Divergence d un champ vectoriel Soit un champ vectoriel v : R 3 R 3 : (x, y, z) v(x, y, z) = (v x, v y, v z ). La divergence est notée symboliquement comme le produit scalaire entre l opérateur Nabla et le champ vectoriel considéré, i.e.. v = v x x + v y + v z. (1.20) y,z y x,z z x,y Tentons de nous donner une image intuitive de la divergence. Pour cela considérons les deux champs vectoriels de la figure 1.2 et calculons leur divergence. Le champ de la figure 1.2(a) est défini par v = (x, y, 0) et le champ de la figure 1.2(b) par v = ( y, x, 0). Nous avons Pour la figure (a) : Pour la figure (b) :. v =.(x, y, 0) = 2. (1.21). v =.( y, x, 0) = 0. (1.22) Ainsi, sur la figure 1.2, la divergence du champ (b) est nulle tandis que la divergence du champ (a) ne l est pas. Nous pouvons donc garder en tête, pour un champ à divergence non nulle, un champ qui rayonne, qui diverge depuis un certain point. Cette image se justifie par un argument beaucoup plus mathématique, le théorème de
8 8 SÉANCE 1. OUTILS MATHÉMATIQUES R R Figure 1.2 Deux champs vectoriels illustrant le concept de divergence et de rotationnel. Le champ vectoriel (a) est d équation v(x, y, z) = (x, y, 0), le second champ vectoriel (b) est d équation v(x, y, z) = ( y, x, 0). Gauss-Ostrograshy qui affirme que le flux du champ v au travers d une surface S fermée, de normale n et sous-tendant un volume V est Φ v = v. n ds =. v dv. (1.23) S Illustrons ce théorème dans le cas de la figure 1.2(a), en considérant une surface S cylindrique, de rayon R, de hauteur h et centrée en l origine. Le terme de surface est normalement composé de trois termes, les deux disques fermant le dessus et le dessous du cylindre mais aussi la surface du cylindre lui-même. Comme n et v ne sont parallèles que sur la surface du cylindre, seul ce terme est non nul. Ainsi, l intégrale de surface devient ˆ ˆ v. n ds = v ds = x2 + y 2 ds. (1.24) Passant en coordonnées cylindriques, il vient S surf.cyl. ˆ 2π ˆ h 0 0 V surf.cyl. R 2 dθ dz = 2πhR 2. (1.25) Le terme de volume s évalue comme suit, en coordonnées cylindriques, et en utilisant le résultat (1.21), V. v dv = ˆ R ˆ 2π ˆ h rdr dθ dz, (1.26) = 2 R2 2π h, 2 (1.27) = 2πhR 2. (1.28) Ainsi, le théorème est illustré. Le théorème de Gauss-Ostrogradsky se retrouve dans de nombreux domaines de la physique, mécanique quantique (conservation de la probabilité), mécanique des fluides (conservation de la masse), électromagnétisme (théorème de Gauss),... Rotationnel d un champ vectoriel Cette section consacrée au rotationnel peut-être ignorée dans le cadre du cours pratique de thermodynamique. Sa présence dans ce manuscrit est seulement due à un soucis de complétude dans l étude de l opérateur Nabla. Reprenons le champ vectoriel v = (v x, v y, v z ) définit dans le cadre de l étude de la divergence. Le rotationnel d un champ vectoriel est noté symboliquement comme le produit vectoriel entre l opérateur Nabla et le champ considéré. v = ( v z y v y, v x v z, v y v x ). (1.29) x,z z x,y z x,y x y,z x y,z y x,z Remarquons que ce résultat est un vecteur. Une autre notation, moins formelle, est souvent utilisée. Celle-ci repose sur la définition de déterminant de matrice. Nous avons
9 1.1. RAPPELS 9 e x e y e z v =... x y,z x y,z z v x v y v z x,y. (1.30) Suivant la philosophie de la section précédente, tentons de nous offrir une image d un rotationnel. Pour cela, revenons vers les deux champs de la figure 1.2 et calculons leur rotationnel. Pour la figure (a) : Pour la figure (b) : v = (x, y, 0) = (0, 0, 0). (1.31) v = ( y, x, 0) = (0, 0, 2). (1.32) Ainsi, seul le vecteur issu du calcul du rotationnel du champ tournant n est pas nul. Ainsi, un champ ayant un rotationnel non nul peut être imaginer comme un champ dont les vecteurs tournent, créent une circulation dans l espace. A l instar de la divergence, cette assertion se justifie par un raisonnement plus mathématique, à savoir, le théorème de Stokes-Green. Ce théorème affirme que la circulation du champ vectoriel v le long d une courbe fermée C est égale au flux du rotationnel du champ v au travers d une surface ouverte S, de normale n, sous-tendue par C. Cela s exprime par v. dl = ( v). n ds. (1.33) C S Illustrons le théorème avec le champ de la figure 1.2(b) en utilisant un cercle de rayon R centré en l origine sous-tendant un disque. Le terme de circulation est, en coordonnées cylindriques, est C v. dl = ˆ 2π Quant au terme de flux, toujours en coordonnées cylindriques 0 (0, R, 0).(0, R dθ, 0) = 2πR 2. (1.34) S ( v). n ds = ˆ R ˆ 2π 0 0 2r dr dθ, (1.35) = 2 R2 2π, 2 (1.36) = 2πR 2. (1.37) Ce qui suffit. Ce théorème se retrouve, par exemple, en électromagnétisme (lois de Maxwell) ou encore en mécanique des fluides (théorème de Stokes),... Laplacien d un champ scalaire Certains lecteurs attentifs auront remarqué que le résultat du gradient était de nature vectorielle (et définit donc un champ vectoriel). Il est donc naturel de se demander quel est le résultat de l application de la divergence sur le gradient d un champ scalaire. Le résultat est la laplacien qui considère les dérivées secondes du champ scalaire. Considérant le champ f introduit dans le cadre de l étude du gradient, nous avons f =. f (1.38) = 2 f x 2 y,z + 2 f y 2 x,z + 2 f z 2 x,y. (1.39) Sans démonstration, nous affirmons que la laplacien évalue la courbure locale moyenne d une fonction. Cet opérateur se retrouve dans de nombreuses lois thermodynamiques comme la loi de Fourier ou encore la loi de Fick.
10 10 SÉANCE 1. OUTILS MATHÉMATIQUES Dérivées secondes Les dérivées partielles d une fonction de plusieurs variables peuvent être combinées entre elles afin de dériver une fonction à plusieurs ordres (comme dans le cas du laplacien) mais aussi selon plusieurs directions. Pour illustrer nos propos, reprenons la fonction f : R 2 R : (x, y) f(x, y) déjà utilisée à la section et, par facilité, notons f/ x y comme f/ x et f/ y x comme f/ y. Ainsi, l expression évalue la dérivée selon x de la dérivée selon y de f. De plus, l expression f x y = 2 f x y, (1.40) f y x = 2 f y x, (1.41) évalue la dérivée selon y de la dérivée selon x de f. Cependant, le théorème de Schwartz affirme que nous avons la relation 2 f y x = 2 f x y. (1.42) Finalement, une matrice peut-être créée, contenant comme élément toutes dérivées secondes d une fonction f. Dans notre cas, nous avons 2 f H[f] = x 2 2 f y x 2 f x y 2 f. (1.43) y 2 Il s agit de la matrice hessienne de f. En particulier, par le théorème de Schwartz, cette matrice est symétrique. De plus, la trace de cette matrice n est autre que le laplacien de f, i.e. Tr(H[f]) = f. (1.44) Développement en série de Taylor Soit f : R R : x f(x) une fonction réelle, x 0 un réel et x une variation du paramètre x autour de x 0, le développement de Taylor de f autour de x 0 est donné, au second ordre, par f(x 0 + x) = f(x 0 ) + x df + 1 dx x=x0 2 x2 d2 f x=x0 dx 2 + O(3), (1.45) où O(3) désigne les termes d ordre x 3 ou plus. Dans le cadre d un développement considérant tout les ordres de la fonction, nous avons f(x 0 + x) = n=0 x n n! Dans le cas d un champ scalaire de n variable, le développement à l ordre 3 s écrit n f x n x=x0. (1.46) f(x 1,0 + x 1,..., x n,0 + x n ) = f(x 1,0,..., x n,0 ) (1.47) f f + x x n x 1 x2=x 2,0,... x n x1=x 1,0, ( x 2 2 f 2 f 1 + x 1 x x 2 2 ) f n 2 x 1 x 2 x 2 1 x 2 n (1.48) (1.49) + O(3). (1.50) Sous une forme plus condensée, nous avons, avec les notations précédemment définies, x 0 = (x 1,0,..., x n,0 ) et x = ( x 1,..., x n ) f( x 0 + x) = f( x 0 ) + x. f x= x x.h[f] x= x 0. x + O(3). (1.51)
11 1.1. RAPPELS Différentielles inexactes Après ces rappels sur les notions de dérivées et de différentielles, une question peut être posée : Est-il toujours possible de décomposer une fonction sous la forme d une différentielle totale comme nous l avons fait à l équation (1.9)? La réponse est non. En effet, une telle décomposition suppose la propriété suivante : il faut que l évaluation de la différence infinitésimale df soit indépendante du chemin choisi pour son évaluation. Tâchons d illustrer cela par un exemple. Soit une fonction f de deux variables dont la différentielle est donnée par la relation (1.9). Nous pouvons l évaluer de deux manières. Soit nous gardons y constant et faisons varier x, nous fixons ensuite x pour varier y, soit l inverse, fixer x pour faire varier y et ensuite garder y constant pour changer x. Les résultats obtenus selon les deux méthodes sont identiques selon la relation (1.9). De manière plus générale, ce sera la cas pour tout chemin utilisé pour évaluer df. Cependant, il existe des fonctions g dont l évaluation de la différentielle dépend du chemin. Traditionnellement, nous notons ces différentielles, nommées différentielles inexactes, par δg. Tâchons de donner un exemple intuitif d une telle fonction et mettons la en parallèle d une fonction dont la différentielle est exacte. Imaginons une montagne, deux personnes veulent en atteindre le sommet : un alpiniste chevronné et un randonneur moins enclin à l escalade. Deux chemins sont possibles pour ces deux personnes : le flan de la montagne, en ligne droite de la base de la montagne à son sommet, et un chemin de promenade tranquille allant en spiralant autour de la montagne. L alpiniste choisit le flan, plus direct, tandis que le randonneur choisit le chemin de promenade, plus long mais moins ardu. Chacun part du même point. Revenons aux mathématiques et définissons deux fonctions : f qui sera la hauteur parcourue et g qui sera la distance parcourue. Pour nos deux protagonistes, la fonction f est identique. En effet, ils partent du même point (la base de la montagne) pour atteindre un même point (son sommet). L évaluation de la fonction f ne dépendant pas du chemin, sa différentielle est exacte. A l inverse, la fonction g est différente pour chaque personnage, l alpiniste allant en ligne droite de la base au sommet et le randonneur en spiralant autour de la montagne le long du chemin de promenade. Le second parcourt donc une distance plus longue que le premier. Ainsi, la fonction g n est pas la même pour l alpiniste que pour le randonneur bien qu ils viennent du même point et arrivent au même point. L évaluation de cette fonction dépend du chemin utilisé et g est décrit par une différentielle inexacte. Afin de donner un critère pour connaître l exactitude ou l inexactitude de la différentielle d une fonction, nous donnons le théorème suivant, généralisable à n dimensions, sans démonstration. Différentielle exacte d une fonction. Une différentielle df = M(x, y)dx + N(x, y)dy est exacte si n importe laquelle des conditions suivantes est satisfaite : L intégrale de f est indépendante du chemin, i.e. df = f(b) f(a). a L intégrale de f sur un contour fermé est nulle, i.e. df = 0 M = N, i.e. la matrice hessienne est symétrique. y x x y Transformation de Legendre La manière traditionnelle de représenter une fonction f : R R : x f(x) se fait par un ensemble de points (x,f(x)) dans un repère cartésien. Le but d une transformation est d encoder les informations contenues dans une fonction sous une autre forme. En effet, il existe, en physique, une multitude de situations où une transformation est employée : en thermodynamique, en mécanique analytique ou encore en traitement du signal. Nous pouvons citer comme exemple de transformation la transformation de Fourier. Celle-ci considère la fonction f(x) comme une superposition de fonctions trigonométriques et encode les informations contenues dans la fonction initiale sous la forme de couples (ω,a(ω)). Ces couples représentent l amplitude A et la fréquence angulaire ω des fonctions trigonométriques intervenant dans la superposition. Un exemple est donné sur la figure 1.5 avec la fonction sin(5x). La transformation de Legendre possède la même philosophie : encoder dans une nouvelle fonction que nous appellerons g(k) les données présentes dans la fonction initiale f(x). Avant d expliciter l encodage qu elle considère, nous nous pencherons sur sa définition puis sur ses diverses propriétés. La transformation de Legendre d une fonction f : A R : x f(x) convexe sur A R est la fonction ˆ b
12 12 SÉANCE 1. OUTILS MATHÉMATIQUES () (ω) - - ω Figure 1.3 A gauche, la fonction sin(5x) encodée dans un repère carthésien et à droite sa transformation de Fourier dans un repère (ω,a) indiquant une fréquence ω = 5 à une amplitude A = 1. () -() () Figure 1.4 Intreprétation géométrique de la transformation de Legendre. g : A R : k g(k) = sup{kx f(x)}. (1.52) x A Cette expression s interprète comme suit : pour une valeur de k donnée, nous recherchons la valeur de x qui maximisera la différence kx f(x). Implicitement, x dépend donc de k. Nous pouvons raffiner la définition (1.52) de la transformation de Legendre en se souvenant que maximiser une expression correspond à annuler sa dérivée. Ainsi, nous obtenons, en annulant la dérivée de kx f(x) par rapport à x, k = df. (1.53) dx Notons que ce maximum existe compte tenu de la convexité de f(x) et qu il est unique pour la même raison. La définition de la transformation peut alors s exprimer comme g(k) = kx(k) f(x(k)) où k = df dx, (1.54) où les dépendances de x ont été clairement explicitées afin de n avoir, pour la fonction g, qu une fonction ne dépendant plus que de k. Nous pouvons désormais interpréter géométriquement la transformation de Legendre. En effet, inversant la relation (1.54), nous avons f(x) = kx g(k) où k = df dx. (1.55) La figure 1.4 illustre cette dernière relation. Sachant que k = df/dx, la droite kx g(k) est tangente à la fonction f(x). De plus, l ordonnée à l origine de cette droite correspond à l opposé de g(k). Ainsi, nous encodons les informations contenues dans la fonction f sous la forme de couples de points (k,g(k)), le premier étant la tangente à la fonction d origine et le second étant l intersection (au signe moins près) de cette tangente avec l axe des ordonnées.
13 1.2. EXERCICES Figure 1.5 A gauche, la fonction x (en bleu) et sa transformation de Legendre x 2 /4 1 (en rouge). A droite, la re-création de la fonction x à partir de sa transformation en utilisant un fuseau de tangentes définies selon la relation (1.55). Sans démonstration, nous donnons la propriété suivante : la double application de la transformation de Legendre permet de revenir à la fonction initiale. Mathématiquement, si t(s) est la transformation de Legendre de g(k) t(s) = sk(s) g(k(s)) où s = dg dk, (1.56) la fonction t est alors égale en tout point à la fonction f. Illustrons maintenant le concept de transformation de Legendre avec un exemple concret. Soit la fonction f(x) = x Afin de déterminer sa transformation, il nous faut obtenir k et pour ensuite obtenir x(k) et finalement appliquer la relation (1.54). L expression de k s obtient par dérivation de f Ainsi, nous obtenons k = df = 2x. (1.57) dx Appliquons maintenant la formule (1.54) pour déterminer la transformation g(k) x = k 2. (1.58) Ses deux fonctions sont illustrées sur le figure Exercices g(k) = kx(k) f(x(k)), (1.59) = k k 2 (k2 4 = k ), (1.60) 1. (1.61) Math-1 Calculez la différentielle exact de l énergie mécanique d une particule en mouvement dans un champ de gravité constant g. Quand le mouvement se fera-t-il à énergie constante? Math-2 Sachant que le potentiel électrique autour d un dipôle est donné par V ( r) = 1 4πɛ 0 d. r r 3, où d est le moment dipolaire électrique et r la distance au centre du dipôle, déterminez l expression de la force que ressentirait une charge test q placée à proximité du dipôle. Math-3 L énergie potentielle d une masse m, placée à une distance r du centre de la Terre de masse M T s exprime comme U(r) = GmM T r Par un développement en série de Taylor, démontrez que près de la surface de la Terre (de rayon R T ), l énergie potentielle croît avec la hauteur h par rapport au.
14 14 SÉANCE 1. OUTILS MATHÉMATIQUES sol comme U(h) = U 0 + mgh, où U 0 et g sont des constantes à déterminer. Depuis les expressions de U(r) et de U(h), dérivez les forces appliquée à la masse m. Trans-1 Démontrer la propriété suivante des transformations de Legendre : dg/dk = x(k). Souvenez-vous pour cela que la dépendance de x a été clairement explicitée. Trans-2 Déterminer la transformation de Legendre i) de l énergie cinétique en cherchant à remplacer v. ii) de l énergie potentielle élastique en cherchant à remplacer x.
15 Séance 2 Calorimétrie & Dilatation 2.1 Rappels Calorimétrie La quantité de chaleur δq à apporter/soustraire à une substance pour augmenter/diminuer sa température d une quantité dt s exprime comme δq = cmdt, (2.1) où c est la capacité calorifique massique de la substance (en J/kg.K) et m sa masse (en kg) et dt (en C ou en K). Il est courant d exprimer cette relation en terme de mol et non en terme de masse, nous avons alors δq = c ndt, (2.2) où c est la capacité calorifique molaire (en J/mol.K) et n est le nombre de mols considéré. La relation suivante est immédiate c = c M (2.3) avec M la masse molaire de la substance. Les relations (2.1) et (2.2) ne sont plus valables lorsque la substance change d état. En effet, dans le cas de l eau, un apport en chaleur fait fondre la glace sans faire varier sa température. De manière similaire, une perte en chaleur fait geler l eau sans en descendre la température. Mathématiquement, nous avons Q = ml, (2.4) Où L est la chaleur latente relative au changement d état (fusion, évaporation, sublimation) et s exprime en J/kg et Q la quantité de chaleur nécessaire au changement d état. Comme dans le cas de l équation (2.1), il existe une formule analogue considérant le nombre de mols et non la masse. Concrètement, les expériences de calorimétrie se réalisent dans le cadre de systèmes thermiquement isolés, c est-à-dire ne pouvant échanger de chaleur avec l extérieur. Ainsi, si deux corps A et B de température différente se trouvent mis en contact, ceux-ci échangeront entre eux des quantités de chaleur Q A B et Q B A telles que Q A B + Q B A = 0. (2.5) Cette équation traduit la conservation de l énergie thermique au sein du système étudié. Notons qu il peut s agir de chaleur due à un changement de température aussi bien que de chaleur due à un changement d état Dilatation Tous corps soumis à un changement de température voit sa taille augmenter. Dans le cas de systèmes linéaires (uni-dimensionnels), cette dilatation s exprime sous forme différentielle comme dl L = αdt, (2.6) 15
16 16 SÉANCE 2. CALORIMÉTRIE & DILATATION où α est le coefficient de dilatation (linéique) en K 1, dt est la variation de température, L la longueur et dl la variation de longueur due à la variation de température. Cette relation a un équivalent dans le cas de systèmes plans (bi-dimensionnels) et de volumes (tri-dimensionnels). Les relations sont ds = γdt, (2.7) S dv = βdt. (2.8) V Dans ces deux dernières formules, β et γ sont respectivement le coefficient de dilatation volumique et le coefficient de dilatation surfacique, tout deux exprimés en K 1. La variable S représente la surface de l objet soumis à la variation de température et V son volume. Notons qu il est possible de démontrer un lien entre les trois coefficients de dilatation précédemment présentés dans le cas de faibles variations de température. En effet, 2.2 Exercices β 3α, (2.9) γ 2α. (2.10) Cal-1 La capacité calorifique molaire d une certaine substance varie avec la température selon la relation suivante c(t ) = 29.5 J/mol.K + ( J/mol.K 2 ) T Quelle est la chaleur nécessaire pour augmenter la température de 3 mols de cette substance de 27 C à 227 C? Cal-2 A très basse température, la capacité calorifique molaire du sel varie selon la loi de Debye c(t ) = k T 3 θ 3, où k = 1940 J/mol.K et θ = 281 K. i) Quelle quantité de chaleur est nécessaire pour élever la température de 1.50 mols de sel de 10 K à 40 K? ii) Quelle est la capacité calorifique moyenne dans cet intervalle de température? iii) Quelle est la capacité calorifique exacte à 40 K? Cal-3 Un bêcher isolé thermiquement et de masse négligeable contient 250 g d eau à la température de 75 C. Combien de kilogrammes de glace à -20 C devront être mélangés à l eau pour abaisser la température à 30 C?(L fus = J/kg, c H20 = 4190 J/kg.K et c glace = 2100 J/kg.K) Cal-4 A quelle vitesse doit-on tirer une balle de plomb de 25 C pour qu elle fonde à l impact? Négligez toutes pertes énergétiques possibles (déformation, émission d ondes sonores, etc.) (L fus = J/kg, T fus = K et c plomb = 130 J/kg.K) Cal-5 Un récipient dont les parois sont thermiquement isolées contient un mélange de 2.4 kg d eau et de 0.45 kg à une température de 0 C. Une chaudière connectée par un tube au récipient injecte de la vapeur à 100 C à la pression atmosphérique. Combien de grammes de vapeur seront nécessaires pour élever la température du mélange eau/glace à 28 C? (L vap = J/kg) Cal-6 Un calorimètre en cuivre de 446 g contient 95 mg de glace. L ensemble est à 0 C. (c cuivre = 390 J/kg) i) Si 35 mg de vapeur à 100 C sont injecté à pression atmosphérique dans le calorimètre, quelle sera la température finale du calorimètre et de son contenu? ii) A cette température finale, combien a-t-on de kilogramme de glace, d eau et de vapeur? Négligez la pression de vapeur saturante. Cal-7 Répondez à la question suivante : Quelle brûlure sera la plus sévère, une brûlure à la vapeur ou une brûlure à l eau bouillante? Pour cela, proposez un petit modèle mathématique qui illustrera vos propos. Cal-8 Répondez à la question suivante : Pourquoi souffler sur sa nourriture pour la refroidir? Etablissez un petit modèle mathématique mettant en évidence l efficacité d un tel procédé. Dil-1 A 10 C, un rail de chemin de fer a une longueur de 30 m. Sachant qu ils sont fait d acier (α= / C), calculez l espacement minimal entre les rails successifs pour que la voie reste utilisable lors de variations de température de ±40 C. Dil-2 A une température T, deux mêmes poutres en acier (α= / C) sont posées horizontalement pour faire un pont de 250 m de long. Aucun espace n est prévu pour la dilatation et les extrémités du pont sont fixes. Si la température augmente, la dilatation va provoquer une déformation verticale. Quelle sera la valeur de l élévation du point de jonction des poutres lorsque la température augmente de 20 C?
17 2.2. EXERCICES 17 Dil-6 Chauffer ou refroidir un matériau dont les extrémités sont fixes mène à l existence d une contrainte dite thermique au sein du matériau, c est à dire une force par unité de surface non nulle. i) Expliquez l existence d une telle contrainte. ii) Démontrez la formule permettant de relier la contrainte thermique au module d Young E du matériau et à la variation de température dt. Dil-7 Les extrémités d une tige d acier (α= / C) sont fixes. Quelle est la contrainte thermique dans la tige lorsque la température baisse de 80 K? Le module de Young de l acier est de E= N/m 2. Figure 2.1 Exercice Dil-2 Dil-3 Un thermomètre à mercure (β= / C) est réalisé à partir d un tube de verre de 10 µm de diamètre intérieur qui se termine par une extrémité sphérique de 2.5 mm de diamètre intérieur. Initialement, le mercure remplit tout juste la sphère. De quelle hauteur le mercure s élève-t-il dans le tube lorsque la température augmente de 1 C? (Nous négligerons la dilatation thermique du verre). Dil-8 Exprimez l angle de courbure θ d un bilame en fonction de L 0 (la longueur à la température T 0, i.e. un bilame non courbé), de T (l écart de température par rapport à T 0 ), de α 1 et de α 2 (les coefficients de dilatation thermique des deux lames) et de r = r 2 r 1 (l écart entre les lames). Figure 2.3 Exercice Dil-8 Figure 2.2 Exercice Dil-3 Dil-4 Une citerne à mazout en acier (α= / C) de forme cubique est calibrée à 10 C pour une capacité de 1m 3. Elle est remplie à ras bord au petit matin, alors que la température ambiante vaut justement 10 C. Au milieu de l après-midi, la température ambiante est de 35 C. Calculez la fraction totale de mazout qui s est échappée par le trop-plein. On donne β= / C. Dil-5 Une horloge à pendule a une tige en laiton (α= / C) dont la période d oscillation vaut 2 s à 20 C. Si la température s élève à 30 C, de combien l horloge va-t-elle retarder ou avancer en une semaine? Dil-9 Une masse de 250 kg est suspendue à un câble de cuivre. Dans son mode fondamental, la corde oscille à la fréquence de 440 Hz. Vous augmentez la température du câble de 40 C. i) De combien la fréquence du mode fondamental va-telle changer? Augmente-t-elle? Décroît-elle? ii) De quel pourcentage la célérité des ondes le long du câble va-t-elle changer? iii) Même question pour la longueur d onde du mode fondamental. Dil-10 Démontrez que le coefficient de dilatation thermique d un gaz parfait est β = 1/T où T est la température du gaz en Kelvin. (β = 1 V ) V T p
18 18 SÉANCE 2. CALORIMÉTRIE & DILATATION
19 Séance 3 Transformations & Machines thermiques 3.1 Rappels Transformations d une gaz Transformations isobares Les transformations isobares sont les transformations au cours desquelles la pression du gaz est maintenue constante et où seuls le volumes et la température varient. Figure 3.1 Transformation isobare à pression p 0, amenant le système du volume V i au volume V f. Notons que la température varie elle aussi, passant de T i à T f. Une telle transformation est représentée par un trait horizontal dans le diagramme PV de la figure 3.1 dans le cas d un gaz parfait. Sachant la pression, le volume et la température des états initial et final, nous pouvons calculer la quantité de chaleur et le travail échangé durant le processus. ˆ Vf W = pdv = p (V f V i ), V i = nk B (T f T i ). (3.1) Q = U W = d 2 nk b(t f T i ) + nk b (T f T i ), = d nk B(T f T i ). (3.2) 19
20 20 SÉANCE 3. TRANSFORMATIONS & MACHINES THERMIQUES La dernière égalité découle de l équation d état des gaz parfaits. Notons que l expression de la chaleur échangée est obtenue en utilisant le premier principe de la thermodynamique U = W +Q et le théorème de l équipartition de l énergie U = d/2 nk b (T f T i ) où d compte le nombre de degrés de liberté d un atome/molécule au sein du gaz parfait. Remarquons finalement que la relation (3.2) aurait aussi pu s écrire sous la forme Q = c p n(t f T i ), (3.3) qui est celle utilisée en calorimétrie. Celle-ci offre aussi l avantage d être valable pour tous les types de gaz. Transformations isochores A l instar des transformations isobares, où la pression est constante, les transformations isochores considèrent des transformations à volume constant. Une illustration est donnée sur la figure 3.2 où le système est amené de la pression p i à la pression p f sans voir son volume changer, en suivant un trait vertical. Cela implique une variation de température allant de T i à T f. Figure 3.2 Transformation isochore au volume V 0, amenant le système de la pression p i à la pression p f. Notons que la température varie elle aussi, passant de T i à T f. Comme dans le cadre des transformations isobares, les échanges énergétiques, en terme de chaleur échangée ou de travail, peuvent être évalués. ˆ Vf W = pdv = 0. (3.4) V i Q = U = d 2 nk B(T f T i ). (3.5) Le système n effectue aucun travail face à la pression extérieure, son volume ne variant pas. Nous obtenons alors aisément la chaleur échangée, en considérant à nouveau le premier principe de la thermodynamique et le théorème d équipartition de l énergie. Comme dans le cadre de transformations isobares, cette dernière relation peut s exprimer différemment comme Q = c v n(t f T i ). (3.6) Comme précédemment, cette relation ne se limite pas aux gaz parfaits mais est valable pour tous types de gaz.
21 3.1. RAPPELS 21 Figure 3.3 Transformation isotherme à la température T 0, amenant le système de la pression p i à la pression p f et le volume de la valeur V i à la valeur V f. Dans le cas d un gaz parfait, cette transformation est donnée par une branche d hyperbole. Transformations isothermes Ce type de transformation s effectue à température constante. Une conséquence directe est que l énergie interne du gaz est inchangée durant un tel processus. U = 0 (3.7) Cette assertion se démontre en utilisant le théorème de l équipartition de l énergie. A ce titre, les transformations isothermes peuvent être qualifiées "d iso-énergétiques". Une seconde conséquence, valable uniquement dans le cas de gaz parfaits, est de rendre le produit pv constant. Ainsi, le courbe isotherme d un gaz parfait dans un diagramme pv est une branche d hyperbole comme l illustre la figure 3.3. Le travail échangé peut être facilement évalué dans le cas d un gaz parfait. En effet, nous avons ˆ Vf ˆ Vf nk b T W = pdv = V i V i V dv, ( ) Vf = nk B T ln, V i ( ) Vf = p i V i ln. (3.8) La chaleur échangée s obtient grâce à la relation (3.7) et du premier principe de la thermodynamique. V i Q = W, = p i V i ln ( Vf V i ). (3.9) Il est très important de constater que la chaleur échangée n est pas nulle, comme nous aurions pu le penser d un point de vue calorimétrique, la température ne variant pas. Transformations adiabatiques Ce dernier type de transformation s effectue sans chaleur échangée. Dès lors, utilisant la relation de Clausius dans le cadre de transformations réversibles, nous pouvons affirmer que les transformations adiabatiques conservent l entropie ds = δq rev T = 0, (3.10)
22 22 SÉANCE 3. TRANSFORMATIONS & MACHINES THERMIQUES T mesurant la température à laquelle s effectue processus. Etant donné la conservation de l entropie, ces transformations sont parfois qualifiées "d iso-entropiques". Figure 3.4 Transformation adiabatique (Q = 0). Dans ce cas, pression, volume et température varient. Dans le cas d un gaz parfait, cette transformation est donnée par une équation de la forme pv γ = cste. La forme d une adiabatique dans un diagramme PV peut s évaluer dans le cas d un gaz parfait. En effet, nous savons par le premier principe de la thermodynamique, par le théorème de l équipartition de l énergie et par l hypothèse de transformation adiabatique que δw = pdv, = d 2 nk BdT. (3.11) Nous pouvons alors écrire que Après intégration, nous obtenons dv V = d dt 2 T. (3.12) ( Vi où encore, grâce à l équation d état des gaz parfaits V f ) 2 ( ) d Tf =, (3.13) T i ( Vi V f ) 2+d d = ( pf p i ), (3.14) ce qui se réécrit sous la forme pv γ = cste, (3.15) γ = 2 + d d. (3.16) Ici, γ porte le nom de coefficient adiabatique. La courbe décrivant un processus adiabatique est proche d une branche d hyperbole (i.e. une isotherme) si ce n est qu elle sera toujours plus pentue, la valeur de γ étant toujours strictement supérieure à 1. Une illustration est donnée sur la figure 3.4. Les échanges énergétiques se trouvent alors aisément. Q = 0 (3.17)
23 3.1. RAPPELS Machines thermiques W = d 2 nk B(T f T i ) = d 2 (p f V f p i V i ) (3.18) Les machines thermiques consistent en une succession de transformations créant un cycle fermé (i.e. ramenant au terme de chaque cycle le système dans son état d origine). De ce fait, l entropie de l univers et l énergie interne, toutes deux variables d état, ne varient pas une fois un cycle terminé Deux types de machines thermiques sont envisageables. Cycles moteurs U = 0 (3.19) S = 0 (3.20) Les cycles moteurs correspondent à des machines pouvant libérer un travail exploitable (i.e. W < 0). Les moteurs diesel et essence sont les archétypes même des machines thermiques basées sur des cycles moteurs. Le fonctionnement de ces machines est schématiquement simple : De la chaleur Q h est pompée par le système depuis une source dite chaude, le moteur transforme partiellement cette chaleur en travail exploitable W et expulse le chaleur Q c qu il n a pas pu convertir vers une source dite froide. La mesure de la qualité d un moteur se fait au travers de son rendement ρ = travail exploitable chaleur injectée, = W Q h. (3.21) La valeur absolue qui entoure W sert à se soustraire de son signe négatif. Sachant que l énergie interne est une variable d état et utilisant le premier principe de la thermodynamique, il vient ρ = 1 Q c Q h. (3.22) Remarquons que cette quantité sera toujours inférieure à 1, ce qui signifie que l énergie ne peut se créer d elle même. Cycles récepteurs Les cycles récepteurs reçoivent du travail pour déplacer des quantités de chaleurs issues de sources froides vers des sources chaudes. Les exemples élémentaires de telles machines sont les réfrigérateurs ou encore les pompes à chaleur, le travail dans ce cas est plus électrique que mécanique. A l instar des moteurs, la qualité d un récepteur se quantifie par son efficacité. Cependant, selon le système considéré, la définition de ce coefficient peut changer. En effet, Dans le cas de frigos : la but est de pomper du chaud" dans le frigo pour le réinjecter hors de celui-ci et ainsi en refroidir le contenu. L efficacité du frigo mesurera donc la quantité de chaleur Q c prise au frigo par rapport au travail injecté W. η = chaleur pompée travail injecté, = Q c W. (3.23) Dans le cas de pompes à chaleur : la but est de pomper du chaud" dans l atmosphère pour le réinjecter dans une pièce et ainsi en réchauffer le contenu, l atmosphère étant plus froide que la pièce considérée. L efficacité de la pompe mesurera donc la quantité de chaleur Q h prise par rapport au travail injecté W. η = chaleur pompée travail injecté, = Q h W. (3.24)
24 24 SÉANCE 3. TRANSFORMATIONS & MACHINES THERMIQUES Chacun de ces coefficients peut être supérieur à l unité. 3.2 Exercices Mach-1 Démontrez, par deux approches différentes, qu un cycle moteur constitué d une isotherme et d une adiabatique ne peut exister. [] () Mach-2 Soit un gaz parfait. i) Proposez une différentielle δq pour la quantité de chaleur échangée lors d une transformation quelconque. ii) Considérez deux points A et B situés sur une même courbe isotherme. Interprétez géométriquement la quantité de chaleur échangée dans les cas suivants : a) une transformation isotherme menant le système de A vers B b) une transformation isobare puis isochore menant le système de A vers B Mach-3 Soit un moteur diesel caractérisé par le cycle de la figure 3.5. Ce moteur se distingue par un très haut taux de compression V A /V B =20 qui permet le processus d auto-inflammation propre aux moteurs diesels. En A, au début du cycle de compression, 500 cm 3 de gaz sont à une température de 27 C et à une pression de 100 kpa. Après la phase de combustion, au début de l expansion adiabatique, la température est de 1500 C. Considérez le gaz comme parfait diatomique. Figure 3.6 Exercice Mach-4 [] Calculez le rendement du cycle. L air est assimilé à un gaz parfait diatomique. Pour cela, nous donnons P A = 2 bar, V A = 2 l, T A = 600 K, V C = 3 l et P C = 1.2 bar. Mach-5 Le rapport de compression d un cycle d Otto est de V A /V B = 8. En A, au début du cycle de compression, 500 cm 3 de gaz parfait diatomique est à une température de 20 C et à une pression de 1bar. Au début de l expansion adiabatique, la température est de T C =750 C. [ ] [ ] Figure 3.5 Exercice Mach-3 Figure 3.7 Exercice Mach-5 i) Calculez le travail échangé entre le système et l extérieur ainsi que les échanges de chaleur lorsque le cycle est parcouru une fois. ii) Calculez le rendement du cycle. iii) Trouvez le nombre de tours/minute qu un tel moteur doit atteindre pour fournir une puissance de 3kW. iv) Indiquez sur le schéma les transformations menant à des absorptions/libérations de travail/chaleur. i) Calculez le travail échangé entre le système et l extérieur ainsi que les échanges de chaleur lorsque le cycle est parcouru une fois. ii) Calculez le rendement du cycle. iii) Trouvez le nombre de tours/minute qu un tel moteur doit atteindre pour fournir une puissance de 1kW. Mach-4 Nous faisons subir le cycle de transformations de la figure 3.6 à de l air. Calculez le travail échangé entre le système et l extérieur ainsi que les échanges de chaleur lorsque le cycle est parcouru une fois. Mach-6 Une mole de gaz parfait monoatomique est soumise à un cycle constitué de deux isochores et de deux isobares. Initialement, la pression, le volume et la température valent respectivement P 0, V 0, T 0.
25 3.2. EXERCICES 25 [ ] Mach-8 Une mole d un gaz parfait décrit, dans le sens trigonométrique, un cycle comportant succesivement une adiabatique réversible, une isobare et une isotherme réversible. On part de A à la température T A, la mole occupant le volume V A pour arriver en B où cette mole occupe un volume V B. On désignera par P A, V A, T A (resp. P B, V B, T B, P C, V C, T C ) les pression, volume et température du point A (resp. B et C). [ ] Figure 3.8 Exercice Mach-6 i) L énergie totale entrant sous forme de chaleur par cycle. ii) L énergie totale sortant sous forme de chaleur par cycle. iii) Le rendement du moteur fonctionnant sur ce cycle. iv) Le rendement d un moteur fonctionnant entre les mêmes températures extrémales avec un cycle de Carnot. Mach-7 Une quantité d air (supposé gaz parfait diatomique) est soumis au cycle moteur suivant. Cette quantité d air subit diverses transformations représentées sur le diagramme PV de la figure 3.9. Le cycle commence au point A où P=10 5 Pa et V=0.25 l. On sait aussi que V B =2 l, V C =1 l et que T D =1000 K. i) Déterminez, au cours d un cycle, le travail fourni par le gaz et ses échanges de chaleur avec l extérieur. ii) Calculez le rendement d une telle machine. iii) Discutez un cycle de Carnot entre les deux mêmes températures extrêmes. [ ] Figure 3.9 Exercice Mach-7 [] Figure 3.10 Exercice Mach-8 i) Calculez P A puis T B, P B, T C, V C et P C en fonction des données T A, V A, V B et γ. ii) Calculez, pour chacune des branches du cycle, le travail et la chaleur reçu par le gaz. Donner le signe de ces 6 grandeurs. iii) Le système fonctionnant comme une pompe à chaleur, sur quelle branche du cycle pompe-t-il de la chaleur? Où en cède-t-il? iv) Quel est le travail total reçu par le gaz lors du cycle? On exprimera le résultat en fonction de c p, T A et T B. v) Définir le coefficient de performance de cette machine et le calculer. Mach-9 Dans un diagramme (T,S), donnez l équation générale i) d une isobare. ii) d une isochore. Mach-10 Dans une pièce totalement isolée de l extérieur (et ne pouvant donc échanger de la chaleur), un frigo fonctionne et est laissé la porte ouverte. La température de la pièce s élève-t-elle ou décroît-elle? Pourquoi?
26 26 SÉANCE 3. TRANSFORMATIONS & MACHINES THERMIQUES Ce tableau résumé l essentiel des informations relatives aux transformations d un gaz parfait Graphique Equation Travail Chaleur p = cste W = p(v f V i ) Q = d p(v f V i ) V = cste W = 0 Q = d 2 (p f p i )V ( ) pv = cste Vf W = p i V i ln V i Q = p i V i ln ( Vf V i ) pv γ = cste W = d 2 (p f V f p i V i ) Q = 0
27 Séance 4 Elements de physique statistique 4.1 Rappels Éléments de statistique et probabilité Nous reprendrons ici quelques notions élémentaires de statistique nécessaires pour la suite de ce chapitre. Les différents résultats et énoncés sont repris de [1]. Principe fondamental de dénombrement. Si r expériences doivent être réalisées et sont telles que la première peut produire l un quelconque des n 1 résultats, si pour chacun d entre eux il y a n 2 résultats possibles pour la deuxième expérience, si pour chaque résultats des deux premières expériences il y a n 3 résultats possibles pour la troisième expérience, et ainsi de suite, il y aura alors un total de n 1.n 2.n 3... n r résultats pour les r expériences prises ensembles. Selon un langage plus symbolique, si Ω désigne le nombre de résultats possibles au terme de r expériences r Ω = n 1.n 2.n 3... n r = n i (4.1) Permutations d objets discernables. Le nombre de permutation de n objets discernables est n! où la factorielle de n est définie comme n! = n.(n 1).(n 2) Permutations d objets partiellement indiscernables. Il y a n! n 1!n 2!... n r! permutations différentes de n objets parmi lesquels n 1 sont indiscernables entre eux, n 2 autres sont indiscernables entre eux,... et n r sont indiscernables entre eux. Combinaisons & coefficient binomial. Le nombre de combinaisons de r objets parmi n est ( ) n n! = r r!(n r)! C est encore le nombre de groupes de taille r si, dans le choix, l ordre n est pas significatif. Combinaisons & coefficient multinomial. Le coefficient ( ) n n! = n 1, n 2,..., n r n 1!n 2!... n r! représente le nombre de répartitions possibles de n objets en r groupes distincts de tailles respectives n 1, n 2,..., n r L entropie de Boltzmann A l inverse de l entropie de Clausius, qui adopte une point de vue macroscopique, l entropie de Boltzmann adopte un point de vue microscopique et intrinsèquement statistique. Celle-ci est définie comme i=1 S = k B log(ω) (4.2) où Ω est appelé nombre de complexion et compte le nombre de configurations différentes discernables au sein du système. 27
28 28 SÉANCE 4. ELEMENTS DE PHYSIQUE STATISTIQUE 4.2 Exercices Stat-1 La notion d information est intrinsèquement liée à celle d entropie. En effet, une configuration microscopique (i.e. microétat) peut servir à coder une information. Dès lors, n microétats peuvent coder n informations différentes et cela crée une entropie importante compte tenu de la formule de Boltzmann. i) Évaluez le nombre de microétats quantiques possibles de 1 mg d eau donc l entropie est de 70 J/mol/K ii) Évaluez l entropie de la Bibliothèque Nationale de France si celle-ci possède volumes de 500 pages avec 1000 symboles sur chacune. iii) Évaluez l entropie de l ADN humain si celui-ci comprend bases où 4 choix sont possibles sur chaque base. iv) Évaluez l entropie du cerveau possèdant neurones pouvant créer une synapse avec 1000 autres neurones. Chaque synapse peut coder l une des deux informations on et off. Représentez sur une échelle logarithmique l ordre de grandeur de chaque entropie évaluée. Stat-2 En partant de la relation entre le nombre de complexion et l entropie, calculez, à l équilibre, la répartition de n molécules sur un sous-réseau de m sites au sein d un réseau de M sites contenant N molécules en tout. Supposez n, m, N et M très grands avec les hypothèses n < m, N < M et m < M. Stat-3 Soit un réseau triangulaire de N 0 sites contenant trois gaz (avec respectivement N 1, N 2 et N 3 molécules). Sachant que le réseau est entièrement rempli des molécules des trois gaz, calculez, à l équilibre, le nombre de complexion d un tel système ainsi que les conditions nécessaires pour maximiser l entropie de Boltzmann. Stat-4 Entropie de mélange Soit deux compartiments, noté 1 et 2, possédant M 1 et M 2 sites partiellement occupés par N 1 et N 2 particules respectivement. Les systèmes sont supposés à l équilibre et séparés l un de l autre par une membrane imperméable. Nous retirons cette membrane pour permettre aux deux compartiments de communiquer. Le système trouve alors un nouvel état d équilibre, les particules pouvant avoir quitté leur compartiment initial pour se retrouver dans l autre, mélangeant ainsi le système. Montrez, en utilisant l entropie de Boltzmann, que dans la variation d entropie du système est donnée par ( ) ( )) N1 + N 2 N1 + N 2 S M = k B (N 1 ln + N 2 ln N 1 N 2
29 Séance 5 Potentiels et équilibres thermodynamiques 5.1 Rappels Différentielle exacte de l énergie interne et équations d état Nous savons que l énergie interne d un système s exprime en terme ses paramètres extensifs : l entropie S, le volume V et le nombre de particules N. Nous ne considérons ici que le cas de base, à trois variables. Nous pourrions aussi imaginer que l énergie interne dépende d autres variables telles que l aire A su système, sa charge q, son aimentation M,.... Dans le cas énoncé, nous avons alors U U(S, V, N). (5.1) Sachant que la variation de l énergie interne est décrite par une différentielle exacte, nous pouvons écrire que du = U ds + U dv + U dn; (5.2) S V,N V S,N N S,V où chacun des termes décrit l évolution de l énergie par la variation seule de l entropie, du volume et du nombre de particules respectivement. Cependant, les deux premiers principes de la thermodynamique nous permettent d affirmer que dans le cas de transformations réversibles du = T ds pdv + µdn, (5.3) où µ désigne le potentiel chimique du système, c est à dire, la contribution d un seul élément à l énergie interne du système sans considérer les éventuelles interactions au sein du système. Par simple comparaison des équations (5.2) et (5.3), nous avons les relations suivantes dites équations d état U = T, (5.4) S V,N U = p, (5.5) V S,N U = µ. (5.6) N S,V Transformation de Legendre et potentiels thermodynamiques Énergie libre F De par sa définition utilisant l entropie, l énergie interne ne peut être mesurée (il n existe pas d entropimètre). Afin de remédier à ce problème, il est courant de considérer le transformation de Legendre de l énergie interne qui est une fonction définie par la température du système et non par son entropie. La transformation de Legendre de l énergie interne (par rapport à la température) se définit comme F (T, V, N) = U(T, V, N) U S(T, V, N). (5.7) S V,N Remarquons que la fonction F dépend maintenant de la température et non plus de l entropie. Sachant l équation (5.4), nous avons 29
30 30 SÉANCE 5. POTENTIELS ET ÉQUILIBRES THERMODYNAMIQUES F (T, V, N) = U(T, V, N) T S(T, V, N). (5.8) La fonction F est qualifiée de potentiel thermodynamique et porte le nom d énergie libre. Il s agit de la fonction à utiliser lorsqu un système est décrit au travers de sa température T, de son volume V et de son nombre de particule N. La différentielle de l énergie libre se calcule aisément à partir de celle de l énergie interne du df = du T ds SdT = T ds pdv + µdn T ds SdT = SdT pdv + µdn (5.9) Cependant, l énergie libre est aussi décrit par une différentielle exacte. Mathématiquement, nous avons donc df = F T V,N dt + F V dv + F T,N N Comparant les équations (5.9) et (5.10), nous obtenons de nouvelles équations d état dn (5.10) T,V Ce potentiel est omniprésent en physique statistique. F = S (5.11) T V,N F = p (5.12) V T,N F = µ (5.13) N T,V Enthalpie G Par simple soucis de confort, il est préférable parfois d exprimer l énergie du système en terme de la pression et non du volume. La transformation de Legendre permet de créer une fonction G(S, p, N) dite enthalpie où encore énergie libre de Gibbs qui remplit ce rôle. Nous la définissons comme suit G(S, p, N) = U(S, p, N) U V (S, p, N) V S,N (5.14) = U(S, p, N) + pv (S, p, N) (5.15) Sa différentielle est dg = du + pdv V dp = T ds pdv + µdn + pdv V dp = T ds + V dp + µdn (5.16) Un calcul, identique à ceux précédemment effectués, nous permet de trouver les équations d état associées à l enthalpie. G = T (5.17) S p,n G = V (5.18) p S,N G = µ (5.19) N S,p Ce potentiel est fort utilisé en chimie, où beaucoup de réactions se font au travers d un contrôle de la pression.
31 5.1. RAPPELS 31 Enthalpie libre H L enthalpie G est décrite par l entropie et est donc sujette au problème évoqué dans le cas de l énergie interne. Afin de d obtenir une fonction décrivant un système en terme de sa température, de sa pression et de son nombre de particules, nous calculons la transformation de Legendre de l enthalpie G par rapport à la température. Nous définissons alors l enthalpie libre H = H(T, p, N) H(T, p, N) = G(T, p, N) G S(T, p, N) S p,n (5.20) = G(T, p, N) T S(T, p, N) (5.21) Sa différentielle est Et les équations d état qui lui sont associées dh = dg T ds SdT = T ds pdv + µdn T ds SdT = SdT + V dp + µdn (5.22) H = S (5.23) T p,n H = V (5.24) p T,N H = µ (5.25) N T,p Ce potentiel est encore fort utilisé en chimie, car il donne l avantage d utiliser la température au lieu de l entropie. C est aussi le potentiel de prédilection des météorologues. Grand potentiel J Le dernier potentiel utilisé est le grand potentiel J(T, V, µ). Il est défini comme la transformation de Legendre de F par rapport au nombre de particules. J(T, V, µ) = F (T, V, µ) F N(T, V, µ) N T,V (5.26) = F (T, V, µ) µn(t, V, µ) (5.27) Sa différentielle est dj = df µdn Ndµ Et finalement, les équations d état qui en découle = SdT pdv + µdn µdn Ndµ = SdT pdv Ndµ (5.28) J = S (5.29) T V,µ J = p (5.30) V T,µ J = N (5.31) µ T,V Ce potentiel se retrouve en physique statistique où il décrit les échanges de particules entre systèmes.
32 32 SÉANCE 5. POTENTIELS ET ÉQUILIBRES THERMODYNAMIQUES μ μ Figure 5.1 Lorsque le système et l environnement qui l entoure est à l équilibre thermodynamique, l entropie de l univers est maximale Équilibres thermodynamiques Tentons de déterminer les conditions d équilibre d un système lorsqu il est mis au contact de son environnement. Pour se faire, nous savons par le second principe de la thermodynamique que, à l équilibre, l univers possède un entropie maximale. Ainsi, si nous décomposons cet univers en deux parties : notre système et l environnement qui l entoure, nous avons le schéma de la figure 5.1. Si l entropie de l univers est extrémale, sachant que l entropie est une quantité extensive, nous pouvons affirmer que où encore, sachant la différentielle exacte de l entropie ds univers = d(s syst + S env ) = 0, (5.32) 1 du syst p syst dv syst + µ syst dn syst + (5.33) T syst T syst T syst 1 du env p env dv env + µ env dn env = 0. T env T env T env Il faut cependant se souvenir de la nature extensive des variables U, V et N. En effet, nous avons U univers = U syst + U env = cste, (5.34) V univers = V syst + V env = cste, (5.35) N univers = N syst + N env = cste, (5.36) l énergie, le volume et le nombre de particule de l univers étant constants si nous faisons l hypothèse qu il s agit d un système isolé. La différentielle de ces expressions donne les liens suivants du syst + du env = 0, (5.37) dv syst + dv env = 0, (5.38) dn syst + dn env = 0. (5.39) Sachant ces contraintes, que ni l énergie du système ou de l environnement ne peut varier sans affecter l autre, de même pour le volume et le nombre de particules, l expression (5.33) devient ( 1 1 ) ( psyst du syst p ) ( env µsyst dv syst + µ ) env dn syst = 0. (5.40) T syst T env T syst T env T syst T env (5.41) Dès lors, nous avons les trois conditions d équilibre thermodynamique.
33 5.2. EXERCICES 33 T syst = T env Equilibre thermique, p syst = p env Equilibre mécanique, µ syst = µ env Equilibre chimique. Ce raisonnement n a pour but que d illustrer la méthode permettant de déterminer les conditions d équilibre d un système face à son environnement. Il doit être adapté au problème considéré en utilisant les potentiels et les effets physiques impliqués. 5.2 Exercices Pot-1 Le terme qui correspond au travail dans le premier principe de la thermodynamique peut être généralisé à d autres effets que la pression. Évaluez son expression i) Dans le cas où le système est soumis à une force quelconque? Explicitez le cas particulier d une force de rappel due à un ressort. ii) Dans le cas où il existe une tension superficielle et que la surface peut changer? iii) Dans le cas où règne un potentiel électrique et qu une charge doit être ajoutée? Pour chaque cas, donner les équations d état de l énergie interne. Pot-2 Nous considérons, pour simplifier, que l air peut être assimilé à un gaz parfait monoatomique (atomes identiques de masse m et sans interaction). Nous voulons construire un modèle d atmosphère isotherme, où toutes les couches d air sont à l équilibre, à la température T. Nous prenons en compte le champ de pesanteur en écrivant qu à l altitude z, l énergie d un atome de vitesse v s écrit : S(U, V, N) = 3Nk b 2 ln ( ) U + KN 2 N ( V Nv0 + Nk b ln N V + 3Nk b 2 ) + 5Nk b 2 ( m ) ln 3π 2 Donnez les équations d état pour ce modèle. En déduire le lien existant entre T, p et v N = V/N. Pot-4 i) Montrez que les capacités calorifiques à volume constant c v = T ( S/ T ) V,N et à pression constante c p = T ( S/ T ) p,n sont égales à une dérivée de l énergie interne pour la première et de l enthalpie pour la seconde. ii) Montrez qu elles sont aussi directement liées à une dérivée seconde de l énergie libre pour c v et de l enthalpie libre pour c p. iii) Utilisez le résultat précédent pour exprimer ( c v / V ) T,N et ( c p / p) T,N à partir de l équation d état f(p, V, N, T ) = 0 du système considéré. ɛ = 1 2 mv2 + mgz Nous isolons une couche d air de volume V contenant N atomes à l altitude z et on donne S(U, V, N, z) = 3Nk b 2 + 3Nk b 2 ( U Nmgz ln N ( m ) ln 3π 2 + 5Nk b 2 ) ( ) V + Nk b ln N i) Déduire les équations d états. Nous écrirons le potentiel chimique en fonction de T, p et z. ii) Deux couches situées à des altitudes différentes sont supposées à la même température. Montrez que ceci implique que l énergie cinétique par atome est la même. iii) Deux couches situées à des altitudes différentes peuvent échanger des atomes. Nous posons donc que le potentiel chimique est indépendant de z. En déduire que la pression diminue exponentiellement avec l altitude. Pot-3 Nous donnons l expression de l entropie pour un gaz de Van der Waals : Pot-5 Quelle est la variation de volume d une sphère métallique lorsque, à la température T et à la pression p, nous la portons au potentiel φ? Nous donnons la capacité d une sphère (C = 4πɛ 0 R) et sa compressibilité isotherme (χ T = (1/V )( V/ p) T ). Calculez la variation relative de volume dans le cas où R = 1cm, χ T = P a 1 et φ = 10 6 V. Pot-6 Lors d une transformation réversible et isotherme, un système reçoit le travail W rev. Reliez W rev à la variation d énergie libre F. Pot-7 L électrostriction Nous considérons les dispositifs de la figure 5.2 comportant un condensateur plan d aire A 0 dont l interdistance entre les plaques sera notée d. L espace entre les armatures, de volume V 0 = A 0 d, est totalement rempli par un fluide diélectrique liquide. L ensemble est maintenu à pression et température constante par un piston diatherme mobile. La permittivité ɛ du diélectrique est fonction de sa température T et de sa masse volumique ρ, ainsi ɛ = ɛ(ρ, T ). Nous prendrons pour hypothèse que ( ɛ/ ρ) T > 0. Nous noterons V le volume du diélectrique et χ T = (1/V )( V/ p) T sa compressibilité isotherme. Nous noterons q la charge
34 34 SÉANCE 5. POTENTIELS ET ÉQUILIBRES THERMODYNAMIQUES portée par le condensateur et φ le potentiel auquel il est porté. Nous noterons aussi C sa capacité électrostatique. le résultat obtenu. Même question pour la seconde géométrie pour laquelle la distance d est libre de varier. Discutez la résultat obtenu. Évaluez les échanges de chaleur (échanges supposés avoir été effectués de manière réversible) dans chaque cas. Equil-1 Loi de Laplace Nous considérons une bulle de savon sphérique de rayon R dans l atmosphère. Nous poserons la tension superficielle de l enveloppe de la bulle comme σ, la température de l atmosphère comme T 0 et la pression externe comme p 0. Nous supposerons que la bulle contient n de gaz parfait. i) Établir les conditions d équilibre thermique et mécanique au sein de la bulle. Étudier l équilibre mécanique dans le cas d une bulle savonneuse (σ = N/m) de 1 cm de rayon dans une atmosphère à 1 bar de pression. ii) Montrer qu il existe toujours un seul rayon d équilibre et en déterminer la valeur. Figure 5.2 Exercice Pot-7 Nous considérons les systèmes formés du diélectrique liquide et du condensateur plan. A l aide de la fonction thermodynamique adaptée, montrez que dans les deux géométries considérées, les dérivées ( V/ φ) p,t et ( S/ φ) p,t s expriment en fonction des dérivées de la capacité électrostatique C du condensateur. Nous considérons la première géométrie proposée ci-dessus, pour laquelle la distance d entre les plaques est fixée. Calculez, en la supposant petite, la variation de volume V du diélectrique lorsque la différence de potentiel entre les armatures du condensateur passe de O à φ. Discutez Equil-2 Nous cherchons les conditions d équilibre d une bulle sphérique, contenant n moles de gaz parfait et dont l enveloppe conductrice porte une charge électrique q. La bulle se trouve dans l atmosphère (à la température T 0 et à la pression p 0 ). Nous désignerons par σ 0 la tension superficielle en l absence de charge. Nous rappellerons la capacité d une sphère conductrice C = 4πɛ 0 R. i) Montrer que la constante de tension superficielle dépend de la charge. Considérer pour cela la température, le volume de la sphère comme invariants. ii) Déterminer les conditions d équilibre de la bulle chargée. Vérifier qu il y a toujours une seule valeur de son rayon, et une seule, qui satisfait à cette condition.
35 Séance 6 Mélanges et changements de phase 6.1 Rappels Mélanges Le fait de mélanger des gaz différents initialement séparés augmente l entropie. Cette augmentation répond à la formule ( ) N1 + N 2 S M = k B N 1 ln + k B N 2 ln N 1 ( N1 + N 2 N 2 ), (6.1) où S M désigne l augmentation d entropie, nommée entropie de mélange, et N 1 et N 2 sont les nombres de molécules de chaque gaz. La croissance de l entropie a pour conséquence de modifier le potentiel chimique de chaque gaz par rapport à la situation où ceux-ci sont isolés l un de l autre. Les équations d état nous permettent de déterminer cette modification S M N i j i = µ M,i T, µ M,i = k B T ln x i, avec µ M,i la contribution au potentiel chimique de l entropie de mélange et x i la fraction molaire du composé i. Ainsi, pour un gaz i à la pression p et température T présent dans un mélange à hauteur de la fraction molaire x i possède un potentiel chimique où µ 0 (p, T ) désigne le potentiel chimique du gaz pris individuellement. µ(p, T, x i ) = µ 0 (p, T ) + k B T ln x i, (6.2) L effet de S M se retrouve dans de nombreuses applications, particulièrement en chimie, dans les phénomènes de pression osmotique, d augmentation ébullioscopique et d abaissement cryoscopique qui découlent de la loi de Raoult ou encore dans la cinétique et l équilibre des réactions chimiques Changements de phase Relation de Clapeyron Intéressons nous désormais aux changements d état. Nous ne nous intéresserons qu aux changements d état entre les trois principaux : solide, liquide et gaz. Les transformations d un état à un autre sont listées à la table 6.1. Ces transformations répondent à la relation de Clapeyron, relation liant la pression et la température de État initial Etat final Gaz Liquide Solide Gaz - Condensation Condensation solide Liquide Ébullition - Solidification Solide Sublimation Fusion - Table 6.1 Table de la nomenclature des changements d état. 35
36 36 SÉANCE 6. MÉLANGES ET CHANGEMENTS DE PHASE Substance p c T c Hydrogène 12.8 atm K Oxygène 49.8 atm K Dioxyde de carbone 72.8 atm K Eau atm K Éthanol atm K Table 6.2 Valeurs de la pression p et de la température T de diverses substances au point critique. Au-delà de ces valeurs, la phase gazeuse et la phase liquide ne peuvent être distinguées l une de l autre. Substance K(L 2 atm/mol 2 ) v 0 (L/mol) Hydrogène Oxygène Dioxyde de carbone Eau Éthanol Table 6.3 Valeurs des constantes K et v 0 du modèle de gaz réels de Van der Waals pour diverses subtances. changement d état à la chaleur latente associée à la transformation et à la variation de volume molaire moyen. Celle-ci s exprime comme dp dt = l T v, (6.3) où l est la chaleur latente par molécule, v la variation élémentaire de volume entre chacune des phases impliquées dans la transformation. Point critique Pour les gaz réels, il existe une valeur de la pression, de la température et du volume au-delà de laquelle un liquide et un gaz sont indiscernables. Cette situation correspond au cas d un fluide super-critique. Dans cet état, la phase gazeuse et liquide sont indiscernables car elles possèdent une même densité, de même indice optique, etc. Dès lors, il est difficile, voire impossible de les distinguer. Le point au-delà duquel le fluide atteint cet état est appelé point critique et est défini, dans un diagramme (p, V ), comme le point d inflexion à tangente nulle de la dernière isotherme du fluide mélangeant phase liquide et phase gazeuse. Mathématiquement, ce point répond aux conditions p = 2 p V pc,v c,t c V pc,v 2 = 0, (6.4) c,t c où p C, V c, T c représentent respectivement la pression, le volume et la température du gaz au point critique. Ces valeurs sont différentes en fonction du gaz étudié. A titre d exemple, sont reprises à la table 6.2 la valeur de la pression et de la température de quelques substances à leur point critique. Divers modèles de gaz réels nous permettent de déterminer analytiquement l expression des coordonnées p, V et T du point critique. Citons par exemple les modèles de Van de Waals, de Dieterici ou encore le développement du Viriel. Dans le cas particulier du gaz de Van de Waals, nous avons, pour (p + KN 2 V 2 )(V Nv 0) = Nk b T, (6.5) (6.6) p C = K, 27v 0 V C = 3Nv 0, (6.7) T C = 8NK, (6.8) 27k B v 0 où v 0 représente un volume exclu dans le système, les particules ne pouvant s interpénétrer, et K une constante représentant l attraction des particules entre-elles due aux interactions au sein du gaz. A nouveau, à titre
37 6.2. EXERCICES 37 d exemple, à la table 6.3, nous donnons les valeurs de K et de v 0 pour diverses substances pour le modèle de Van der Waals. 6.2 Exercices Mél-1 Considérez un mélange de plusieurs gaz parfaits à l équilibre. En utilisant l énergie libre, trouvez l expression de la pression totale et aussi du potentiel chimique de chaque élément. Nous donnons l entropie d un gaz parfait : S(U, V, N) = k b [N ln ( ) V + 3N ( ) U N 2 ln N + 3N 2 ln ( m 3π 2 ) + 5N 2 Mél-2 Soit une réaction chimique du type A+B C, réalisée à pression et température constantes, entre trois gaz supposés parfaits. Nous partons d une situation initiale où seuls A et B sont présents en quantité égale. Exprimez la fraction molaire x A à l équilibre en fonction de la température et des µ i,0, les potentiels chimiques des espèces non mélangées. Mél-3 Loi de Raoult Calculez la dépendance de la pression de vapeur saturant d un solvant selon la concentration d une substance qui y est dissoute. Mettez en évidence la modification de la température d ébullition du solvant. En particulier, augmente t-elle ou diminue t-elle? Phase-1 Recherchez les expressions de la pression, de la température et du volume au point critique d un gaz de Van der Walls et calculez l équation réduite. Quelle est l utilité de l équation réduite? Nous donnons ]. (p + KN 2 V 2 )(V Nv 0) = Nk b T Phase-2 Une personne dont le poids est de 700 N marche sur une patinoire de -0.5 C. i) La surface de contact entre ses pieds et la glace est de 10 2 m 2. La glace va-t-elle fondre sous ses pieds? Justifiez par calcul sachant que la chaleur latente de fusion est de 6000 J/mol, que la variation relative de volume est V/V liq = 9.05% et qu une mole d eau liquide pèse 18 g. ii) Même question pour le même patineur, chaussé cette fois-ci de patins à glace. La surface dans ce cas est alors de 10 4 m 2. Phase-3 M. Vandewalle présente une expérience dans laquelle il coupe un glaçon avec un fil (de masse négligeable) auquel sont attachées deux masses identiques. La glace est à une température T = 5 C, le fil possède un section carrée de 1 mm 2. Sachant que la chaleur latente de fusion est de 6000 J/mol, que la variation de volume lors de la fonte est V = m 3 et que le glaçon est de 5 cm d arête, expliquez son échec. Ne se décourageant pas, il utilise alors un glaçon à T = 0.5 C de 1 cm de côté avec un fil de 0.01 mm 2 de section. Quelle est la valeur des masses qu il doit utiliser dans ce cas? Phase-4 Formule empirique de Rankine Rankine donna une formule empirique de la variation de la pression de vapeur saturante de l eau avec la température. Celle-ci est ln p sat = 5120 T où la température T s exprime en degré Celsius et la pression en atmosphère. Estimez l erreur liée à l utilisation de cette formule à 50 C, sachant que l eau bouille à 100 C à 1 atm et que la chaleur latente de vaporisation de l eau est de kj/kg.
38 38 SÉANCE 6. MÉLANGES ET CHANGEMENTS DE PHASE
39 Bibliographie [1] Sheldon M. Ross, Initiation aux probabilités, Presses polytechniques et universitaires romandes, [2] Greiner Walter, Thermodynamics and Statistical Mechanics, Springer, [3] R. K. P. Zia, E. F. Redish and S. R. McKay, Making sense of the Legendre transform, Am. J. Phys. 77, 7 (2009). [4] H. D. Young and R. A. Freedman, University Physics, Pearson - Addison Wesley, 11 th edition, 2004 [5] R. D. Serway and J. W. Jewett, Physics, Brooks/Cole Cengage Learning, 9 th edition 39
Premier principe : bilans d énergie
 MPSI - Thermodynamique - Premier principe : bilans d énergie page 1/5 Premier principe : bilans d énergie Table des matières 1 De la mécanique à la thermodynamique : formes d énergie et échanges d énergie
MPSI - Thermodynamique - Premier principe : bilans d énergie page 1/5 Premier principe : bilans d énergie Table des matières 1 De la mécanique à la thermodynamique : formes d énergie et échanges d énergie
Fonctions de plusieurs variables
 Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Module : Analyse 03 Chapitre 00 : Fonctions de plusieurs variables Généralités et Rappels des notions topologiques dans : Qu est- ce que?: Mathématiquement, n étant un entier non nul, on définit comme
Exercices - Fonctions de plusieurs variables : corrigé. Pour commencer
 Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
Pour commencer Exercice 1 - Ensembles de définition - Première année - 1. Le logarithme est défini si x + y > 0. On trouve donc le demi-plan supérieur délimité par la droite d équation x + y = 0.. 1 xy
OM 1 Outils mathématiques : fonction de plusieurs variables
 Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.
Outils mathématiques : fonction de plusieurs variables PCSI 2013 2014 Certaines partie de ce chapitre ne seront utiles qu à partir de l année prochaine, mais une grande partie nous servira dès cette année.
Cours d Analyse. Fonctions de plusieurs variables
 Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours d Analyse Fonctions de plusieurs variables Licence 1ère année 2007/2008 Nicolas Prioux Université de Marne-la-Vallée Table des matières 1 Notions de géométrie dans l espace et fonctions à deux variables........
Cours Fonctions de deux variables
 Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
Cours Fonctions de deux variables par Pierre Veuillez 1 Support théorique 1.1 Représentation Plan et espace : Grâce à un repère cartésien ( ) O, i, j du plan, les couples (x, y) de R 2 peuvent être représenté
1 Thermodynamique: première loi
 1 hermodynamique: première loi 1.1 Énoncé L énergie d un système isolé est constante, L énergie de l univers est constante, de univers = de syst + de env. = 0 1 L énergie d un système est une fonction
1 hermodynamique: première loi 1.1 Énoncé L énergie d un système isolé est constante, L énergie de l univers est constante, de univers = de syst + de env. = 0 1 L énergie d un système est une fonction
DYNAMIQUE DE FORMATION DES ÉTOILES
 A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées.
 Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées. 1 Ce sujet aborde le phénomène d instabilité dans des systèmes dynamiques
Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées. 1 Ce sujet aborde le phénomène d instabilité dans des systèmes dynamiques
Premier principe de la thermodynamique - conservation de l énergie
 Chapitre 5 Premier principe de la thermodynamique - conservation de l énergie 5.1 Bilan d énergie 5.1.1 Énergie totale d un système fermé L énergie totale E T d un système thermodynamique fermé de masse
Chapitre 5 Premier principe de la thermodynamique - conservation de l énergie 5.1 Bilan d énergie 5.1.1 Énergie totale d un système fermé L énergie totale E T d un système thermodynamique fermé de masse
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4)
 FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
FONCTIONS DE PLUSIEURS VARIABLES (Outils Mathématiques 4) Bernard Le Stum Université de Rennes 1 Version du 13 mars 2009 Table des matières 1 Fonctions partielles, courbes de niveau 1 2 Limites et continuité
Initiation à la Mécanique des Fluides. Mr. Zoubir HAMIDI
 Initiation à la Mécanique des Fluides Mr. Zoubir HAMIDI Chapitre I : Introduction à la mécanique des fluides 1 Introduction La mécanique des fluides(mdf) a pour objet l étude du comportement des fluides
Initiation à la Mécanique des Fluides Mr. Zoubir HAMIDI Chapitre I : Introduction à la mécanique des fluides 1 Introduction La mécanique des fluides(mdf) a pour objet l étude du comportement des fluides
Chapitre 0 Introduction à la cinématique
 Chapitre 0 Introduction à la cinématique Plan Vitesse, accélération Coordonnées polaires Exercices corrigés Vitesse, Accélération La cinématique est l étude du mouvement Elle suppose donc l existence à
Chapitre 0 Introduction à la cinématique Plan Vitesse, accélération Coordonnées polaires Exercices corrigés Vitesse, Accélération La cinématique est l étude du mouvement Elle suppose donc l existence à
Cours de Mécanique du point matériel
 Cours de Mécanique du point matériel SMPC1 Module 1 : Mécanique 1 Session : Automne 2014 Prof. M. EL BAZ Cours de Mécanique du Point matériel Chapitre 1 : Complément Mathématique SMPC1 Chapitre 1: Rappels
Cours de Mécanique du point matériel SMPC1 Module 1 : Mécanique 1 Session : Automne 2014 Prof. M. EL BAZ Cours de Mécanique du Point matériel Chapitre 1 : Complément Mathématique SMPC1 Chapitre 1: Rappels
3 Approximation de solutions d équations
 3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
Calcul intégral élémentaire en plusieurs variables
 Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Calcul intégral élémentaire en plusieurs variables PC*2 2 septembre 2009 Avant-propos À part le théorème de Fubini qui sera démontré dans le cours sur les intégrales à paramètres et qui ne semble pas explicitement
Oscillations libres des systèmes à deux degrés de liberté
 Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
Chapitre 4 Oscillations libres des systèmes à deux degrés de liberté 4.1 Introduction Les systèmes qui nécessitent deux coordonnées indépendantes pour spécifier leurs positions sont appelés systèmes à
8.1 Généralités sur les fonctions de plusieurs variables réelles. f : R 2 R (x, y) 1 x 2 y 2
 Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Chapitre 8 Fonctions de plusieurs variables 8.1 Généralités sur les fonctions de plusieurs variables réelles Définition. Une fonction réelle de n variables réelles est une application d une partie de R
Fonctions de plusieurs variables
 Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
Maths MP Exercices Fonctions de plusieurs variables Les indications ne sont ici que pour être consultées après le T (pour les exercices non traités). Avant et pendant le T, tenez bon et n allez pas les
NOTICE DOUBLE DIPLÔME
 NOTICE DOUBLE DIPLÔME MINES ParisTech / HEC MINES ParisTech/ AgroParisTech Diplômes obtenus : Diplôme d ingénieur de l Ecole des Mines de Paris Diplôme de HEC Paris Ou Diplôme d ingénieur de l Ecole des
NOTICE DOUBLE DIPLÔME MINES ParisTech / HEC MINES ParisTech/ AgroParisTech Diplômes obtenus : Diplôme d ingénieur de l Ecole des Mines de Paris Diplôme de HEC Paris Ou Diplôme d ingénieur de l Ecole des
Plan du cours : électricité 1
 Semestre : S2 Module Physique II 1 Electricité 1 2 Optique géométrique Plan du cours : électricité 1 Partie A : Electrostatique (discipline de l étude des phénomènes liés aux distributions de charges stationnaires)
Semestre : S2 Module Physique II 1 Electricité 1 2 Optique géométrique Plan du cours : électricité 1 Partie A : Electrostatique (discipline de l étude des phénomènes liés aux distributions de charges stationnaires)
Erratum de MÉCANIQUE, 6ème édition. Introduction Page xxi (milieu de page) G = 6, 672 59 10 11 m 3 kg 1 s 2
 Introduction Page xxi (milieu de page) G = 6, 672 59 1 11 m 3 kg 1 s 2 Erratum de MÉCANIQUE, 6ème édition Page xxv (dernier tiers de page) le terme de Coriolis est supérieur à 1% du poids) Chapitre 1 Page
Introduction Page xxi (milieu de page) G = 6, 672 59 1 11 m 3 kg 1 s 2 Erratum de MÉCANIQUE, 6ème édition Page xxv (dernier tiers de page) le terme de Coriolis est supérieur à 1% du poids) Chapitre 1 Page
Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre
 IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
IUFM du Limousin 2009-10 PLC1 Mathématiques S. Vinatier Rappels de cours Fonctions de plusieurs variables, intégrales multiples, et intégrales dépendant d un paramètre 1 Fonctions de plusieurs variables
Exercice 1. Exercice n 1 : Déséquilibre mécanique
 Exercice 1 1. a) Un mobile peut-il avoir une accélération non nulle à un instant où sa vitesse est nulle? donner un exemple illustrant la réponse. b) Un mobile peut-il avoir une accélération de direction
Exercice 1 1. a) Un mobile peut-il avoir une accélération non nulle à un instant où sa vitesse est nulle? donner un exemple illustrant la réponse. b) Un mobile peut-il avoir une accélération de direction
Précision d un résultat et calculs d incertitudes
 Précision d un résultat et calculs d incertitudes PSI* 2012-2013 Lycée Chaptal 3 Table des matières Table des matières 1. Présentation d un résultat numérique................................ 4 1.1 Notations.........................................................
Précision d un résultat et calculs d incertitudes PSI* 2012-2013 Lycée Chaptal 3 Table des matières Table des matières 1. Présentation d un résultat numérique................................ 4 1.1 Notations.........................................................
Chapitre 11 Bilans thermiques
 DERNIÈRE IMPRESSION LE 30 août 2013 à 15:40 Chapitre 11 Bilans thermiques Table des matières 1 L état macroscopique et microcospique de la matière 2 2 Énergie interne d un système 2 2.1 Définition.................................
DERNIÈRE IMPRESSION LE 30 août 2013 à 15:40 Chapitre 11 Bilans thermiques Table des matières 1 L état macroscopique et microcospique de la matière 2 2 Énergie interne d un système 2 2.1 Définition.................................
Chapitre 4 Le deuxième principe de la thermodynamique
 Chapitre 4 Le deuxième principe de la thermodynamique 43 4.1. Evolutions réversibles et irréversibles 4.1.1. Exemples 4.1.1.1. Exemple 1 Reprenons l exemple 1 du chapitre précédent. Une masse est placée
Chapitre 4 Le deuxième principe de la thermodynamique 43 4.1. Evolutions réversibles et irréversibles 4.1.1. Exemples 4.1.1.1. Exemple 1 Reprenons l exemple 1 du chapitre précédent. Une masse est placée
Chapitre 2 Le problème de l unicité des solutions
 Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Université Joseph Fourier UE MAT 127 Mathématiques année 2011-2012 Chapitre 2 Le problème de l unicité des solutions Ce que nous verrons dans ce chapitre : un exemple d équation différentielle y = f(y)
Plan du chapitre «Milieux diélectriques»
 Plan du chapitre «Milieux diélectriques» 1. Sources microscopiques de la polarisation en régime statique 2. Etude macroscopique de la polarisation en régime statique 3. Susceptibilité diélectrique 4. Polarisation
Plan du chapitre «Milieux diélectriques» 1. Sources microscopiques de la polarisation en régime statique 2. Etude macroscopique de la polarisation en régime statique 3. Susceptibilité diélectrique 4. Polarisation
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
Etudier le diagramme température-pression, en particulier le point triple de l azote.
 K4. Point triple de l azote I. BUT DE LA MANIPULATION Etudier le diagramme température-pression, en particulier le point triple de l azote. II. BASES THEORIQUES Etats de la matière La matière est constituée
K4. Point triple de l azote I. BUT DE LA MANIPULATION Etudier le diagramme température-pression, en particulier le point triple de l azote. II. BASES THEORIQUES Etats de la matière La matière est constituée
TP 7 : oscillateur de torsion
 TP 7 : oscillateur de torsion Objectif : étude des oscillations libres et forcées d un pendule de torsion 1 Principe général 1.1 Définition Un pendule de torsion est constitué par un fil large (métallique)
TP 7 : oscillateur de torsion Objectif : étude des oscillations libres et forcées d un pendule de torsion 1 Principe général 1.1 Définition Un pendule de torsion est constitué par un fil large (métallique)
L énergie sous toutes ses formes : définitions
 L énergie sous toutes ses formes : définitions primaire, énergie secondaire, utile ou finale. Quelles sont les formes et les déclinaisons de l énergie? D après le dictionnaire de l Académie française,
L énergie sous toutes ses formes : définitions primaire, énergie secondaire, utile ou finale. Quelles sont les formes et les déclinaisons de l énergie? D après le dictionnaire de l Académie française,
À propos d ITER. 1- Principe de la fusion thermonucléaire
 À propos d ITER Le projet ITER est un projet international destiné à montrer la faisabilité scientifique et technique de la fusion thermonucléaire contrôlée. Le 8 juin 005, les pays engagés dans le projet
À propos d ITER Le projet ITER est un projet international destiné à montrer la faisabilité scientifique et technique de la fusion thermonucléaire contrôlée. Le 8 juin 005, les pays engagés dans le projet
Chapitre 1 Cinématique du point matériel
 Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Chapitre 1 Cinématique du point matériel 7 1.1. Introduction 1.1.1. Domaine d étude Le programme de mécanique de math sup se limite à l étude de la mécanique classique. Sont exclus : la relativité et la
Cours d électricité. Circuits électriques en courant constant. Mathieu Bardoux. 1 re année
 Cours d électricité Circuits électriques en courant constant Mathieu Bardoux [email protected] IUT Saint-Omer / Dunkerque Département Génie Thermique et Énergie 1 re année Objectifs du chapitre
Cours d électricité Circuits électriques en courant constant Mathieu Bardoux [email protected] IUT Saint-Omer / Dunkerque Département Génie Thermique et Énergie 1 re année Objectifs du chapitre
Continuité et dérivabilité d une fonction
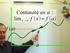 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE
 LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE 2. L EFFET GYROSCOPIQUE Les lois physiques qui régissent le mouvement des véhicules terrestres sont des lois universelles qui s appliquent
LES LOIS PHYSIQUES APPLIQUÉES AUX DEUX-ROUES : 1. LA FORCE DE GUIDAGE 2. L EFFET GYROSCOPIQUE Les lois physiques qui régissent le mouvement des véhicules terrestres sont des lois universelles qui s appliquent
Les Conditions aux limites
 Chapitre 5 Les Conditions aux limites Lorsque nous désirons appliquer les équations de base de l EM à des problèmes d exploration géophysique, il est essentiel, pour pouvoir résoudre les équations différentielles,
Chapitre 5 Les Conditions aux limites Lorsque nous désirons appliquer les équations de base de l EM à des problèmes d exploration géophysique, il est essentiel, pour pouvoir résoudre les équations différentielles,
LA MESURE DE PRESSION PRINCIPE DE BASE
 Page 1 / 6 LA MESURE DE PRESSION PRINCIPE DE BASE 1) Qu est-ce qu un sensor de pression? Tout type de sensor est composé de 2 éléments distincts : Un corps d épreuve soumit au Paramètre Physique φ à mesurer
Page 1 / 6 LA MESURE DE PRESSION PRINCIPE DE BASE 1) Qu est-ce qu un sensor de pression? Tout type de sensor est composé de 2 éléments distincts : Un corps d épreuve soumit au Paramètre Physique φ à mesurer
Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière
 Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière Algèbre 1 : (Volume horaire total : 63 heures) UE1 : Analyse et algèbre
Contenu pédagogique des unités d enseignement Semestre 1(1 ère année) Domaine : Sciences et techniques et Sciences de la matière Algèbre 1 : (Volume horaire total : 63 heures) UE1 : Analyse et algèbre
ANALYSE NUMERIQUE ET OPTIMISATION. Une introduction à la modélisation mathématique et à la simulation numérique
 1 ANALYSE NUMERIQUE ET OPTIMISATION Une introduction à la modélisation mathématique et à la simulation numérique G. ALLAIRE 28 Janvier 2014 CHAPITRE I Analyse numérique: amphis 1 à 12. Optimisation: amphis
1 ANALYSE NUMERIQUE ET OPTIMISATION Une introduction à la modélisation mathématique et à la simulation numérique G. ALLAIRE 28 Janvier 2014 CHAPITRE I Analyse numérique: amphis 1 à 12. Optimisation: amphis
F411 - Courbes Paramétrées, Polaires
 1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié [email protected] http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013
1/43 Courbes Paramétrées Courbes polaires Longueur d un arc, Courbure F411 - Courbes Paramétrées, Polaires Michel Fournié [email protected] http://www.math.univ-toulouse.fr/ fournie/ Année 2012/2013
Optimisation des fonctions de plusieurs variables
 Optimisation des fonctions de plusieurs variables Hervé Hocquard Université de Bordeaux, France 8 avril 2013 Extrema locaux et globaux Définition On étudie le comportement d une fonction de plusieurs variables
Optimisation des fonctions de plusieurs variables Hervé Hocquard Université de Bordeaux, France 8 avril 2013 Extrema locaux et globaux Définition On étudie le comportement d une fonction de plusieurs variables
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications
 Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
TSTI 2D CH X : Exemples de lois à densité 1
 TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
TSTI 2D CH X : Exemples de lois à densité I Loi uniforme sur ab ; ) Introduction Dans cette activité, on s intéresse à la modélisation du tirage au hasard d un nombre réel de l intervalle [0 ;], chacun
Etude de fonctions: procédure et exemple
 Etude de fonctions: procédure et exemple Yves Delhaye 8 juillet 2007 Résumé Dans ce court travail, nous présentons les différentes étapes d une étude de fonction à travers un exemple. Nous nous limitons
Etude de fonctions: procédure et exemple Yves Delhaye 8 juillet 2007 Résumé Dans ce court travail, nous présentons les différentes étapes d une étude de fonction à travers un exemple. Nous nous limitons
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1
 Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
Chafa Azzedine - Faculté de Physique U.S.T.H.B 1 Définition: La cinématique est une branche de la mécanique qui étudie les mouements des corps dans l espace en fonction du temps indépendamment des causes
PHYSIQUE-CHIMIE. Partie I - Propriétés de l atome
 PHYSIQUE-CHIMIE Ce sujet traite de quelques propriétés de l aluminium et de leurs applications. Certaines données fondamentales sont regroupées à la fin du texte. Partie I - Propriétés de l atome I.A -
PHYSIQUE-CHIMIE Ce sujet traite de quelques propriétés de l aluminium et de leurs applications. Certaines données fondamentales sont regroupées à la fin du texte. Partie I - Propriétés de l atome I.A -
COURS DE THERMODYNAMIQUE
 I.U.T. de Saint-Omer Dunkerque Département Génie Thermique et énergie COURS DE THERMODYNAMIQUE eme Semestre Olivier PERROT 010-011 1 Avertissement : Ce cours de thermodynamique présente quelques applications
I.U.T. de Saint-Omer Dunkerque Département Génie Thermique et énergie COURS DE THERMODYNAMIQUE eme Semestre Olivier PERROT 010-011 1 Avertissement : Ce cours de thermodynamique présente quelques applications
U-31 CHIMIE-PHYSIQUE INDUSTRIELLES
 Session 200 BREVET de TECHNICIEN SUPÉRIEUR CONTRÔLE INDUSTRIEL et RÉGULATION AUTOMATIQUE E-3 SCIENCES PHYSIQUES U-3 CHIMIE-PHYSIQUE INDUSTRIELLES Durée : 2 heures Coefficient : 2,5 Durée conseillée Chimie
Session 200 BREVET de TECHNICIEN SUPÉRIEUR CONTRÔLE INDUSTRIEL et RÉGULATION AUTOMATIQUE E-3 SCIENCES PHYSIQUES U-3 CHIMIE-PHYSIQUE INDUSTRIELLES Durée : 2 heures Coefficient : 2,5 Durée conseillée Chimie
Mesure de la dépense énergétique
 Mesure de la dépense énergétique Bioénergétique L énergie existe sous différentes formes : calorifique, mécanique, électrique, chimique, rayonnante, nucléaire. La bioénergétique est la branche de la biologie
Mesure de la dépense énergétique Bioénergétique L énergie existe sous différentes formes : calorifique, mécanique, électrique, chimique, rayonnante, nucléaire. La bioénergétique est la branche de la biologie
MESURE DE LA TEMPERATURE
 145 T2 MESURE DE LA TEMPERATURE I. INTRODUCTION Dans la majorité des phénomènes physiques, la température joue un rôle prépondérant. Pour la mesurer, les moyens les plus couramment utilisés sont : les
145 T2 MESURE DE LA TEMPERATURE I. INTRODUCTION Dans la majorité des phénomènes physiques, la température joue un rôle prépondérant. Pour la mesurer, les moyens les plus couramment utilisés sont : les
Problèmes sur le chapitre 5
 Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Problèmes sur le chapitre 5 (Version du 13 janvier 2015 (10h38)) 501 Le calcul des réactions d appui dans les problèmes schématisés ci-dessous est-il possible par les équations de la statique Si oui, écrire
Chapitre 1 Régime transitoire dans les systèmes physiques
 Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer
Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer
T.P. FLUENT. Cours Mécanique des Fluides. 24 février 2006 NAZIH MARZOUQY
 T.P. FLUENT Cours Mécanique des Fluides 24 février 2006 NAZIH MARZOUQY 2 Table des matières 1 Choc stationnaire dans un tube à choc 7 1.1 Introduction....................................... 7 1.2 Description.......................................
T.P. FLUENT Cours Mécanique des Fluides 24 février 2006 NAZIH MARZOUQY 2 Table des matières 1 Choc stationnaire dans un tube à choc 7 1.1 Introduction....................................... 7 1.2 Description.......................................
GENERALITES SUR LA MESURE DE TEMPERATURE
 Distributeur exclusif de GENERALITES SUR LA MESURE DE TEMPERATURE INTRODUCTION...2 GENERALITES SUR LA MESURE DE TEMPERATURE...2 La température...2 Unités de mesure de température...3 Echelle de température...3
Distributeur exclusif de GENERALITES SUR LA MESURE DE TEMPERATURE INTRODUCTION...2 GENERALITES SUR LA MESURE DE TEMPERATURE...2 La température...2 Unités de mesure de température...3 Echelle de température...3
1 Mise en application
 Université Paris 7 - Denis Diderot 2013-2014 TD : Corrigé TD1 - partie 2 1 Mise en application Exercice 1 corrigé Exercice 2 corrigé - Vibration d une goutte La fréquence de vibration d une goutte d eau
Université Paris 7 - Denis Diderot 2013-2014 TD : Corrigé TD1 - partie 2 1 Mise en application Exercice 1 corrigé Exercice 2 corrigé - Vibration d une goutte La fréquence de vibration d une goutte d eau
1 Définition. 2 Systèmes matériels et solides. 3 Les actions mécaniques. Le système matériel : Il peut être un ensemble.un sous-ensemble..
 1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
1 Définition GÉNÉRALITÉS Statique 1 2 Systèmes matériels et solides Le système matériel : Il peut être un ensemble.un sous-ensemble..une pièce mais aussi un liquide ou un gaz Le solide : Il est supposé
Stockage de chaleur solaire par sorption : Analyse et contrôle du système à partir de sa simulation dynamique
 Stockage de chaleur solaire par sorption : Analyse et contrôle du système à partir de sa simulation dynamique Kokouvi Edem N TSOUKPOE 1, Nolwenn LE PIERRÈS 1*, Lingai LUO 1 1 LOCIE, CNRS FRE3220-Université
Stockage de chaleur solaire par sorption : Analyse et contrôle du système à partir de sa simulation dynamique Kokouvi Edem N TSOUKPOE 1, Nolwenn LE PIERRÈS 1*, Lingai LUO 1 1 LOCIE, CNRS FRE3220-Université
document proposé sur le site «Sciences Physiques en BTS» : http://nicole.cortial.net BTS AVA 2015
 BT V 2015 (envoyé par Frédéric COTTI - Professeur d Electrotechnique au Lycée Régional La Floride Marseille) Document 1 - Etiquette énergie Partie 1 : Voiture à faible consommation - Une étiquette pour
BT V 2015 (envoyé par Frédéric COTTI - Professeur d Electrotechnique au Lycée Régional La Floride Marseille) Document 1 - Etiquette énergie Partie 1 : Voiture à faible consommation - Une étiquette pour
Baccalauréat ES/L Métropole La Réunion 13 septembre 2013 Corrigé
 Baccalauréat S/L Métropole La Réunion 13 septembre 2013 Corrigé A. P. M.. P. XRCIC 1 Commun à tous les candidats Partie A 1. L arbre de probabilité correspondant aux données du problème est : 0,3 0,6 H
Baccalauréat S/L Métropole La Réunion 13 septembre 2013 Corrigé A. P. M.. P. XRCIC 1 Commun à tous les candidats Partie A 1. L arbre de probabilité correspondant aux données du problème est : 0,3 0,6 H
LA PHYSIQUE DES MATERIAUX. Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE
 LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
LA PHYSIQUE DES MATERIAUX Chapitre 1 LES RESEAUX DIRECT ET RECIPROQUE Pr. A. Belayachi Université Mohammed V Agdal Faculté des Sciences Rabat Département de Physique - L.P.M [email protected] 1 1.Le réseau
Repérage d un point - Vitesse et
 PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
PSI - écanique I - Repérage d un point - Vitesse et accélération page 1/6 Repérage d un point - Vitesse et accélération Table des matières 1 Espace et temps - Référentiel d observation 1 2 Coordonnées
Notes du cours MTH1101 Calcul I Partie II: fonctions de plusieurs variables
 Notes du cours MTH1101 Calcul I Partie II: fonctions de plusieurs variables Guy Desaulniers Département de mathématiques et de génie industriel École Polytechnique de Montréal Automne 2014 Table des matières
Notes du cours MTH1101 Calcul I Partie II: fonctions de plusieurs variables Guy Desaulniers Département de mathématiques et de génie industriel École Polytechnique de Montréal Automne 2014 Table des matières
Chapitre 5. Le ressort. F ext. F ressort
 Chapitre 5 Le ressort Le ressort est un élément fondamental de plusieurs mécanismes. Il existe plusieurs types de ressorts (à boudin, à lame, spiral etc.) Que l on comprime ou étire un ressort, tel que
Chapitre 5 Le ressort Le ressort est un élément fondamental de plusieurs mécanismes. Il existe plusieurs types de ressorts (à boudin, à lame, spiral etc.) Que l on comprime ou étire un ressort, tel que
STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE
 ÉCOLE D'INGÉNIEURS DE FRIBOURG (E.I.F.) SECTION DE MÉCANIQUE G.R. Nicolet, revu en 2006 STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE Eléments de calcul vectoriel Opérations avec les forces Equilibre du point
ÉCOLE D'INGÉNIEURS DE FRIBOURG (E.I.F.) SECTION DE MÉCANIQUE G.R. Nicolet, revu en 2006 STATIQUE GRAPHIQUE ET STATIQUE ANALYTIQUE Eléments de calcul vectoriel Opérations avec les forces Equilibre du point
PHYSIQUE Discipline fondamentale
 Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Examen suisse de maturité Directives 2003-2006 DS.11 Physique DF PHYSIQUE Discipline fondamentale Par l'étude de la physique en discipline fondamentale, le candidat comprend des phénomènes naturels et
Vision industrielle et télédétection - Détection d ellipses. Guillaume Martinez 17 décembre 2007
 Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Vision industrielle et télédétection - Détection d ellipses Guillaume Martinez 17 décembre 2007 1 Table des matières 1 Le projet 3 1.1 Objectif................................ 3 1.2 Les choix techniques.........................
Sujet proposé par Yves M. LEROY. Cet examen se compose d un exercice et de deux problèmes. Ces trois parties sont indépendantes.
 Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Promotion X 004 COURS D ANALYSE DES STRUCTURES MÉCANIQUES PAR LA MÉTHODE DES ELEMENTS FINIS (MEC 568) contrôle non classant (7 mars 007, heures) Documents autorisés : polycopié ; documents et notes de
Items étudiés dans le CHAPITRE N5. 7 et 9 p 129 D14 Déterminer par le calcul l'antécédent d'un nombre par une fonction linéaire
 CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
CHAPITRE N5 FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION FONCTIONS LINEAIRES NOTION DE FONCTION Code item D0 D2 N30[S] Items étudiés dans le CHAPITRE N5 Déterminer l'image
Équations non linéaires
 Équations non linéaires Objectif : trouver les zéros de fonctions (ou systèmes) non linéaires, c-à-d les valeurs α R telles que f(α) = 0. y f(x) α 1 α 2 α 3 x Equations non lineaires p. 1/49 Exemples et
Équations non linéaires Objectif : trouver les zéros de fonctions (ou systèmes) non linéaires, c-à-d les valeurs α R telles que f(α) = 0. y f(x) α 1 α 2 α 3 x Equations non lineaires p. 1/49 Exemples et
Calcul différentiel sur R n Première partie
 Calcul différentiel sur R n Première partie Université De Metz 2006-2007 1 Définitions générales On note L(R n, R m ) l espace vectoriel des applications linéaires de R n dans R m. Définition 1.1 (différentiabilité
Calcul différentiel sur R n Première partie Université De Metz 2006-2007 1 Définitions générales On note L(R n, R m ) l espace vectoriel des applications linéaires de R n dans R m. Définition 1.1 (différentiabilité
Différentiabilité ; Fonctions de plusieurs variables réelles
 Différentiabilité ; Fonctions de plusieurs variables réelles Denis Vekemans R n est muni de l une des trois normes usuelles. 1,. 2 ou.. x 1 = i i n Toutes les normes de R n sont équivalentes. x i ; x 2
Différentiabilité ; Fonctions de plusieurs variables réelles Denis Vekemans R n est muni de l une des trois normes usuelles. 1,. 2 ou.. x 1 = i i n Toutes les normes de R n sont équivalentes. x i ; x 2
EXERCICE 2 : SUIVI CINETIQUE D UNE TRANSFORMATION PAR SPECTROPHOTOMETRIE (6 points)
 BAC S 2011 LIBAN http://labolycee.org EXERCICE 2 : SUIVI CINETIQUE D UNE TRANSFORMATION PAR SPECTROPHOTOMETRIE (6 points) Les parties A et B sont indépendantes. A : Étude du fonctionnement d un spectrophotomètre
BAC S 2011 LIBAN http://labolycee.org EXERCICE 2 : SUIVI CINETIQUE D UNE TRANSFORMATION PAR SPECTROPHOTOMETRIE (6 points) Les parties A et B sont indépendantes. A : Étude du fonctionnement d un spectrophotomètre
Les indices à surplus constant
 Les indices à surplus constant Une tentative de généralisation des indices à utilité constante On cherche ici en s inspirant des indices à utilité constante à définir un indice de prix de référence adapté
Les indices à surplus constant Une tentative de généralisation des indices à utilité constante On cherche ici en s inspirant des indices à utilité constante à définir un indice de prix de référence adapté
SUIVI CINETIQUE PAR SPECTROPHOTOMETRIE (CORRECTION)
 Terminale S CHIMIE TP n 2b (correction) 1 SUIVI CINETIQUE PAR SPECTROPHOTOMETRIE (CORRECTION) Objectifs : Déterminer l évolution de la vitesse de réaction par une méthode physique. Relier l absorbance
Terminale S CHIMIE TP n 2b (correction) 1 SUIVI CINETIQUE PAR SPECTROPHOTOMETRIE (CORRECTION) Objectifs : Déterminer l évolution de la vitesse de réaction par une méthode physique. Relier l absorbance
Exercices - Polynômes : corrigé. Opérations sur les polynômes
 Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
PHYSIQUE 2 - Épreuve écrite
 PHYSIQUE - Épreuve écrite WARIN André I. Remarques générales Le sujet de physique de la session 010 comprenait une partie A sur l optique et une partie B sur l électromagnétisme. - La partie A, à caractère
PHYSIQUE - Épreuve écrite WARIN André I. Remarques générales Le sujet de physique de la session 010 comprenait une partie A sur l optique et une partie B sur l électromagnétisme. - La partie A, à caractère
Exemples d utilisation de G2D à l oral de Centrale
 Exemples d utilisation de G2D à l oral de Centrale 1 Table des matières Page 1 : Binaire liquide-vapeur isotherme et isobare Page 2 : Page 3 : Page 4 : Page 5 : Page 6 : intéressant facile facile sauf
Exemples d utilisation de G2D à l oral de Centrale 1 Table des matières Page 1 : Binaire liquide-vapeur isotherme et isobare Page 2 : Page 3 : Page 4 : Page 5 : Page 6 : intéressant facile facile sauf
Le modèle de Black et Scholes
 Le modèle de Black et Scholes Alexandre Popier février 21 1 Introduction : exemple très simple de modèle financier On considère un marché avec une seule action cotée, sur une période donnée T. Dans un
Le modèle de Black et Scholes Alexandre Popier février 21 1 Introduction : exemple très simple de modèle financier On considère un marché avec une seule action cotée, sur une période donnée T. Dans un
Caractéristiques des ondes
 Caractéristiques des ondes Chapitre Activités 1 Ondes progressives à une dimension (p 38) A Analyse qualitative d une onde b Fin de la Début de la 1 L onde est progressive puisque la perturbation se déplace
Caractéristiques des ondes Chapitre Activités 1 Ondes progressives à une dimension (p 38) A Analyse qualitative d une onde b Fin de la Début de la 1 L onde est progressive puisque la perturbation se déplace
DOCM 2013 http://docm.math.ca/ Solutions officielles. 1 2 10 + 1 2 9 + 1 2 8 = n 2 10.
 A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
A1 Trouvez l entier positif n qui satisfait l équation suivante: Solution 1 2 10 + 1 2 9 + 1 2 8 = n 2 10. En additionnant les termes du côté gauche de l équation en les mettant sur le même dénominateur
I - Quelques propriétés des étoiles à neutrons
 Formation Interuniversitaire de Physique Option de L3 Ecole Normale Supérieure de Paris Astrophysique Patrick Hennebelle François Levrier Sixième TD 14 avril 2015 Les étoiles dont la masse initiale est
Formation Interuniversitaire de Physique Option de L3 Ecole Normale Supérieure de Paris Astrophysique Patrick Hennebelle François Levrier Sixième TD 14 avril 2015 Les étoiles dont la masse initiale est
THEME 2. LE SPORT CHAP 1. MESURER LA MATIERE: LA MOLE
 THEME 2. LE SPORT CHAP 1. MESURER LA MATIERE: LA MOLE 1. RAPPEL: L ATOME CONSTITUANT DE LA MATIERE Toute la matière de l univers, toute substance, vivante ou inerte, est constituée à partir de particules
THEME 2. LE SPORT CHAP 1. MESURER LA MATIERE: LA MOLE 1. RAPPEL: L ATOME CONSTITUANT DE LA MATIERE Toute la matière de l univers, toute substance, vivante ou inerte, est constituée à partir de particules
TD 9 Problème à deux corps
 PH1ME2-C Université Paris 7 - Denis Diderot 2012-2013 TD 9 Problème à deux corps 1. Systèmes de deux particules : centre de masse et particule relative. Application à l étude des étoiles doubles Une étoile
PH1ME2-C Université Paris 7 - Denis Diderot 2012-2013 TD 9 Problème à deux corps 1. Systèmes de deux particules : centre de masse et particule relative. Application à l étude des étoiles doubles Une étoile
Notion de fonction. Résolution graphique. Fonction affine.
 TABLE DES MATIÈRES 1 Notion de fonction. Résolution graphique. Fonction affine. Paul Milan LMA Seconde le 12 décembre 2011 Table des matières 1 Fonction numérique 2 1.1 Introduction.................................
TABLE DES MATIÈRES 1 Notion de fonction. Résolution graphique. Fonction affine. Paul Milan LMA Seconde le 12 décembre 2011 Table des matières 1 Fonction numérique 2 1.1 Introduction.................................
Chapitre 3. Quelques fonctions usuelles. 1 Fonctions logarithme et exponentielle. 1.1 La fonction logarithme
 Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Théorème du point fixe - Théorème de l inversion locale
 Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
Chapitre 7 Théorème du point fixe - Théorème de l inversion locale Dans ce chapitre et le suivant, on montre deux applications importantes de la notion de différentiabilité : le théorème de l inversion
CONCOURS COMMUN 2010 PHYSIQUE
 CONCOUS COMMUN SUJET A DES ÉCOLES DES MINES D ALBI, ALÈS, DOUAI, NANTES Épreuve de Physique-Chimie (toutes filières) Corrigé Barème total points : Physique points - Chimie 68 points PHYSIQUE Partie A :
CONCOUS COMMUN SUJET A DES ÉCOLES DES MINES D ALBI, ALÈS, DOUAI, NANTES Épreuve de Physique-Chimie (toutes filières) Corrigé Barème total points : Physique points - Chimie 68 points PHYSIQUE Partie A :
Trépier avec règle, ressort à boudin, chronomètre, 5 masses de 50 g.
 PHYSQ 130: Hooke 1 LOI DE HOOKE: CAS DU RESSORT 1 Introduction La loi de Hooke est fondamentale dans l étude du mouvement oscillatoire. Elle est utilisée, entre autres, dans les théories décrivant les
PHYSQ 130: Hooke 1 LOI DE HOOKE: CAS DU RESSORT 1 Introduction La loi de Hooke est fondamentale dans l étude du mouvement oscillatoire. Elle est utilisée, entre autres, dans les théories décrivant les
Physique : Thermodynamique
 Correction du Devoir urveillé n o 8 Physique : hermodynamique I Cycle moteur [Véto 200] Cf Cours : C P m C V m R relation de Mayer, pour un GP. C P m γr γ 29, 0 J.K.mol et C V m R γ 20, 78 J.K.mol. 2 Une
Correction du Devoir urveillé n o 8 Physique : hermodynamique I Cycle moteur [Véto 200] Cf Cours : C P m C V m R relation de Mayer, pour un GP. C P m γr γ 29, 0 J.K.mol et C V m R γ 20, 78 J.K.mol. 2 Une
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES
 INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
INTRODUCTION À L ANALYSE FACTORIELLE DES CORRESPONDANCES Dominique LAFFLY Maître de Conférences, Université de Pau Laboratoire Société Environnement Territoire UMR 5603 du CNRS et Université de Pau Domaine
t 100. = 8 ; le pourcentage de réduction est : 8 % 1 t Le pourcentage d'évolution (appelé aussi taux d'évolution) est le nombre :
 Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Terminale STSS 2 012 2 013 Pourcentages Synthèse 1) Définition : Calculer t % d'un nombre, c'est multiplier ce nombre par t 100. 2) Exemples de calcul : a) Calcul d un pourcentage : Un article coûtant
Continuité en un point
 DOCUMENT 4 Continuité en un point En général, D f désigne l ensemble de définition de la fonction f et on supposera toujours que cet ensemble est inclus dans R. Toutes les fonctions considérées sont à
DOCUMENT 4 Continuité en un point En général, D f désigne l ensemble de définition de la fonction f et on supposera toujours que cet ensemble est inclus dans R. Toutes les fonctions considérées sont à
Cours IV Mise en orbite
 Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
Introduction au vol spatial Cours IV Mise en orbite If you don t know where you re going, you ll probably end up somewhere else. Yogi Berra, NY Yankees catcher v1.2.8 by-sa Olivier Cleynen Introduction
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1
 La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
La Licence Mathématiques et Economie-MASS Université de Sciences Sociales de Toulouse 1 La licence Mathématiques et Economie-MASS de l Université des Sciences Sociales de Toulouse propose sur les trois
Fonctions de deux variables. Mai 2011
 Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
Fonctions de deux variables Dédou Mai 2011 D une à deux variables Les fonctions modèlisent de l information dépendant d un paramètre. On a aussi besoin de modéliser de l information dépendant de plusieurs
G.P. DNS02 Septembre 2012. Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3. Réfraction
 DNS Sujet Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3 Réfraction I. Préliminaires 1. Rappeler la valeur et l'unité de la perméabilité magnétique du vide µ 0. Donner
DNS Sujet Réfraction...1 I.Préliminaires...1 II.Première partie...1 III.Deuxième partie...3 Réfraction I. Préliminaires 1. Rappeler la valeur et l'unité de la perméabilité magnétique du vide µ 0. Donner
TOUT CE QU IL FAUT SAVOIR POUR LE BREVET
 TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
TOUT E QU IL FUT SVOIR POUR LE REVET NUMERIQUE / FONTIONS eci n est qu un rappel de tout ce qu il faut savoir en maths pour le brevet. I- Opérations sur les nombres et les fractions : Les priorités par
