Complexité. Licence Informatique - Semestre 2 - Algorithmique et Programmation
|
|
|
- Yvette Bonnet
- il y a 9 ans
- Total affichages :
Transcription
1 Complexité Objectifs des calculs de complexité : - pouvoir prévoir le temps d'exécution d'un algorithme - pouvoir comparer deux algorithmes réalisant le même traitement Exemples : - si on lance le calcul de la factorielle de 100, combien de temps faudra t-il attendre le résultat? - quel algorithme de tri vaut-il mieux utiliser pour retrier un tableau où on vient de changer un élément? L'évaluation de la complexité peut se faire à plusieurs niveaux : au niveau purement algorithmique, par l'analyse et le calcul au niveau de l'exécution du programme expérimentalement 1
2 Complexité expérimentale Il est possible d'évaluer de façon expérimentale le temps d'exécution des programmes. Cette évaluation expérimentale dépend beaucoup des langages de programmation, ordinateurs et systèmes d'exploitation utilisés. Pour avoir un sens, l'évaluation expérimentale requiert un étalonnage des ordinateurs utilisés. 2
3 Benchmarking Un logiciel de benchmark (étalonnage) donne une mesure de puissance d'un ordinateur en flops (floating point operations per second). Cette puissance varie en fonction des traitements effectués (calculs bruts, sur des entiers ou des réels, calculs liés à l'affichage,...) Puissance des ordinateurs grand public actuels : quelques Gigaflops (10 6 flops) Puissance des meilleurs super-ordinateurs actuels : environ 1000 Teraflops (10 15 flops) (cf. 3
4 Complexité temporelle vs spatiale (1/2) Exemple : échange de deux valeurs entières // échange des valeurs de deux variables entier x, y, z;... // initialisation de x et y z <- x; x <- y; y <- z; // échange des valeurs de deux variables entier x, y;... // initialisation de x et y x <- y-x; y <- y-x; x <- y+x; - la première méthode utilise une variable supplémentaire et réalise 3 affectations - la deuxième méthode n'utilise que les deux variables dont on veut échanger les valeurs, mais réalise 3 affectations et 3 opérations 4
5 Complexité temporelle vs spatiale (2/2) L'efficacité d'un algorithme peut être évalué en temps et en espace : - complexité en temps : évaluation du temps d'exécution de l'algorithme - complexité en espace : évaluation de l'espace mémoire occupé par l'exécution de l'algorithme Règle (non officielle) de l'espace-temps informatique : pour gagner du temps de calcul, on doit utiliser davantage d'espace mémoire. On s'intéresse essentiellement à la complexité en temps (ce qui n'était pas forcément le cas quand les mémoires coutaient cher) 5
6 Paramètre de complexité (1/3) Le paramètre de la complexité est ce qui va faire varier le temps d'exécution de l'algorithme. Exemple : la calcul de la factorielle fonction avec retour entier factorielle1(entier n) entier i, resultat; début resultat <- 1; pour (i allant de 2 à n pas 1) faire resultat <- resultat*i; finpour retourne resultat; fin Le paramètre de complexité est la valeur de n 6
7 Paramètre de complexité (2/3) Exemple : multiplier tous les éléments d'un tableau d'entiers par un entier donné fonction sans retour multiplie(entier[] tab, int x) entier i; début pour (i allant de 0 à tab.longueur-1 pas de 1) faire tab[i] < tab[i] * x; finpour fin Le paramètre de complexité est la longueur du tableau tab. 7
8 Paramètre de complexité (3/3) Exemple : faire la somme des premiers éléments de chaque ligne d'un tableau à deux dimensions fonction avec retour entier sommeteteligne(entier[][] tab) entier i,s; début s <- 0; pour (i allant de 0 à tab[0].longueur-1 pas de 1) faire s < s + tab[0][i]; finpour retourne s; fin Le seul paramètre de complexité est la longueur de tab[0]. Quand l'algorithme opère sur une structure multidimensionnelle, il faut bien préciser le paramètre de complexité. Un algorithme opérant sur de telles structures peut avoir des complexités différentes selon la dimension considérée. 8
9 Calcul de complexité (1/2) Exemple : la factorielle fonction avec retour entier factorielle1(entier n) entier i, resultat; début resultat <- 1; pour (i allant de 2 à n pas 1) faire resultat <- resultat*i; finpour retourne resultat; fin On peut fixer des temps d'exécution constants à chaque type d'instruction : - affectation d'entier : ae - comparaison d'entier : ce - opération élémentaire sur des entiers : oe On néglige le coût des déclarations, des affectations et du retour. 9
10 Calcul de complexité (2/2) L'exécution de la fonction va prendre : resultat <- 1; ae pour (i allant de 2 à n pas 1) faire resultat <- resultat*i; finpour + (n-1) * (ae + oe) Au total, le temps d'exécution sera de la forme a*n+b a et b dépendent du langage de programmation et de l'ordinateur utilisés. 10
11 Complexité au mieux et au pire (1/4) Exemple : recherche séquentielle d'un élément dans un tableau de n chaines de caractères fonction avec retour booléen rechercheelement(chaine[] tab, chaine x) entier i; début i <- 0; tantque (i < tab.longueur) faire si (tab[i] = x) alors retourne VRAI; finsi fintantque retourne FAUX; fin Le paramètre de complexité est la taille du tableau d'entrée. Le nombre de tours de boucles varie selon que x est dans le tableau ou pas, et selon l'endroit où x est présent. 11
12 Complexité au mieux et au pire (2/4) Si x est dans la première case du tableau : 1 tour de boucle avec la condition tab[i]=x vraie Si x est dans la deuxième case du tableau : 1 tour de boucle avec la condition tab[i]=x fausse et 1 tour de boucle avec la condition tab[i]=x vraie... fonction avec retour booléen rechercheelement(chaine[] tab, chaine x) entier i; début i <- 0; tantque (i < tab.longueur) faire si (tab[i] = x) alors retourne VRAI; finsi fintantque retourne FAUX; fin Si x est dans dernière case du tableau : tab.longueur-1 tours de boucle avec la condition tab[i]=x fausse et 1 tour de boucle avec la condition tab[i]=x vraie Si x n'est pas dans le tableau : tab.longueur tours de boucle avec la condition tab[i]=x fausse 12
13 Complexité au mieux et au pire (3/4) Lorsque, pour une valeur donnée du paramètre de complexité, le temps d'exécution varie selon les données d'entrée, on peut distinguer : - La complexité au pire : temps d'exécution maximum, dans le cas le plus défavorable. - La complexité au mieux : temps d'exécution minimum, dans le cas le plus favorable (en pratique, cette complexité n'est pas très utile). - La complexité moyenne : temps d'exécution dans un cas médian, ou moyenne des temps d'exécution. Le plus souvent, on utilise la complexité au pire, car on veut borner le temps d'exécution. 13
14 Complexité au mieux et au pire (4/4) fonction avec retour booléen rechercheelement(chaine[] tab, chaine x) entier i; début i <- 0; tantque (i < tab.longueur) faire si (tab[i] = x) alors retourne VRAI; finsi i <- i + 1; fintantque retourne FAUX; fin n = la taille du tableau, ae = affectation d'entier, ce = comparaison d'entier, oe=opération sur les entiers. Complexité au pire (x n'est pas dans le tableau) : ae+n*(2*ce+oe+ae) Complexité au mieux (x est dans la première case du tableau) : ae+2*ce Complexité en moyenne : considérons qu'on a 50% de chance que x soit dans le tableau, et 50% qu'il n'y soit pas, et, s'il y est sa position moyenne est au milieu. Le temps d'exécution est [ (ae+n*(2*ce+oe+ae)) + (ae+ (n/2)*(2*ce+oe+ae)) ] /2, de la forme a*n+b (avec a et b constantes) 14
15 Complexité asymptotique (1/4) Calculer la complexité de façon exacte n'est pas raisonnable vu la quantité d'instructions de la plupart des programmes et n'est pas utile pour pouvoir comparer deux algorithmes. Première approximation : on ne considère souvent que la complexité au pire Deuxième approximation : on ne calcule que la forme générale de la complexité Troisième approximation : on ne regarde que le comportement asymptotique de la complexité 15
16 Domination asymptotique (1/2) f et g étant des fonctions, f = O(g) s'il existe des constantes c>0 et n 0 telles que f(x) < c*g(x) pour tout x > n 0 c*g(x) f(x) n 0 x f = O(g) signifie que f est dominée asymptotiquement par g. 16
17 Domination asymptotique (2/2) La notation O, dite notation de Landau, vérifie les propriétés suivantes : - si f=o(g) et g=o(h) alors f=o(h) - si f=o(g) et k un nombre, alors k*f=o(g) - si f1=o(g1) et f2=o(g2) alors f1+f2 = O(g2+g2) - si f1=o(g1) et f2=o(g2) alors f1*f2 = O(g2*g2) Exemples de domination asymptotique : x = O(x 2 ) car pour x>1, x<x 2 x 2 = O(x 3 ) car pour x>1, x 2 <x 3 100*x = O(x 2 ) car pour x>100, x<x 2 ln(x) = O(x) car pour x>0, ln(x)<x si i>0, x i = O(e x ) car pour x tel que x/ln(x)>i, x i <e x Notation Ω : f = Ω(g) s'il existe des constantes c>0 et n 0 telles que f(x) c*g(x) pour tout x n 0 17
18 Equivalence asymptotique f et g étant des fonctions, f = Θ(g) s'il existe des constantes c 1, c 2, strictement positives et n 0 telles que c1*g(x) f(x) c2*g(x) pour tout x n 0 c 2 *g(x) f(x) c 1 *g(x) n 0 x 18
19 Classes de complexité (1/3) O(1) : complexité constante, pas d'augmentation du temps d'exécution quand le paramètre croit O(log(n)) : complexité logarithmique, augmentation très faible du temps d'exécution quand le paramètre croit. Exemple : algorithmes qui décomposent un problème en un ensemble de problèmes plus petits (dichotomie). O(n) : complexité linéaire, augmentation linéraire du temps d'exécution quand le paramètre croit (si le paramètre double, le temps double). Exemple : algorithmes qui parcourent séquentiellement des structures linéaires. O(nlog(n)) : complexité quasi-linéaire, augmentation un peu supérieure à O(n). Exemple : algorithmes qui décomposent un problème en d'autres plus simples, traités indépendaments et qui combinent les solutions partielles pour calculer la solution générale. 19
20 Classes de complexité (2/3) O(n 2 ) : complexité quadratique, quand le paramètre double, le temps d'exécution est multiplié par 4. Exemple : algorithmes avec deux boucles imbriquées. O(n i ) : complexité polynomiale, quand le paramètre double, le temps d'exécution est multiplié par 2 i. Exemple : algorithme utilisant i boucles imbriquées. O(i n ) : complexité exponentielle, quand le paramètre double, le temps d'exécution est élevé à la puissance 2. O(n!) : complexité factorielle, asymptotiquement équivalente à n n Encore pire : la fonction d'ackerman Ack(m,n) = n+1 si m = 0 Ack(m,n) = Ack(m-1,1) si n=0 et m > 0 Ack(m,n) = Ack(m-1, Ack(m,n-1)) sinon Ack(0,0) = 1, Ack(1,1) = 3, Ack(2,2) = 7, Ack(3,3) = 61, Ack(4,4) est supérieur à
21 Classes de complexité (3/3) Les algorithmes de complexité polynomiale ne sont utilisables que sur des données réduites, ou pour des traitements ponctuels Les algorithmes exponentiels ou au delà ne sont pas utilisables en pratique 21
22 Complexité et temps d'exécution Temps de calcul pour des données de taille 1 million complexité flops ln(n) n n² 2 n ,013ms 1s 278 heures ans ,013μs 1ms ¼ heure 10 ans ,013ns 1μs 1s 1 semaine Loi de Moore (empirique) : à coût constant, la rapidité des processeurs double tous les 18 mois (les capacités de stockage suivent la même loi). Constat : le volume des données stockées dans les systèmes d'informations augmente de façon exponentielle. Conclusion : il vaut mieux optimiser ses algorithmes qu'attendre des années qu'un processeur surpuissant soit inventé. 22
23 Recherche séquentielle fonction avec retour booléen rechercheelement(chaine[] tab, chaine x) entier i; début i <- 0; tantque (i < tab.longueur) faire si (tab[i] = x) alors retourne VRAI; finsi i <- i + 1; fintantque retourne FAUX; fin n = la taille du tableau, ae = affectation d'entier, ce = comparaison d'entier, oe = opération sur les entiers. Complexité au pire (x n'est pas dans le tableau) : ae+n*(2*ce+ae+oe) = O(n) Complexité au mieux (x est dans la première case du tableau) : ae+2*ce = O(1) Complexité en moyenne : considérons qu'on a 50% de chance que x soit dans le tableau, et 50% qu'il n'y soit pas, et, s'il y est sa position moyenne est au milieu. Le temps d'exécution est [ (ae+n*(2*ce+oe+ae)) + (ae+ (n/2)*(2*ce+oe+ae)) ] /2, de la forme a*n+b (avec a et b constantes) = O(n) 23
24 Recherche dichotomique (1/2) fonction avec retour booléen recherchedicho(chaine[] tab, chaine x) entier i, j; début i <- 0; j <- tab.longueur-1; tantque (i <= j) faire si (tab[(j+i)/2] = x) alors retourne VRAI; sinon si (tab[(j+i)/2] > x) alors j <- (j+i)/2-1; sinon i <- (j+i)/2 + 1; finsi finsi fintantque retourne FAUX; fin Le paramètre de complexité est la longueur du tableau, qu'on appelle n. Cas au pire : x n'est pas dans le tableau. La longueur de la partie du tableau comprise entre i et j est d'abord n, puis n/2, puis n/4,..., jusqu'à ce que n/2 t = 1. Le nombre de tours de boucles est donc un entier t tel que n/2 t = 1 soit 2 t = n soit t*log(2) = log(n) soit t = log 2 (n) 24
25 Recherche dichotomique (2/2) fonction avec retour booléen recherchedicho(chaine[] tab, chaine x) entier i, j; début i <- 0; j <- tab.longueur-1; tantque (i <= j) faire si (tab[(j+i)/2] = x) alors retourne VRAI; sinon si (tab[(j+i)/2] > x) alors j <- (j+i)/2-1; sinon i <- (j+i)/2 + 1; finsi finsi fintantque retourne FAUX; fin La complexité au pire de la recherche dichotomique est (ce + 2* cc + 3*oe)*log 2 (n) avec ce = comparaison d'entier, cc = comparaison de chaine, oe = opération élémentaire. Complexité asymptotique : O(log(n)) Conclusion : pour des données de grande taille, si le tableau est trié, il vaut mieux utiliser la recherche dichotomique 25
26 Factorielle récursive (1/2) Exemple : calcul récursif de la factorielle // cette fonction renvoie n! (n est supposé supérieur ou égal à 1) fonction avec retour entier factorielle2(entier n) début si (n = 1) alors retourne 1; sinon retourne n*factorielle2(n-1); finsi fin Paramètre de complexité : la valeur de n Il n'y a qu'un seul cas d'exécution (pas de cas au pire ou au mieux) Si n 1, le calcul de la factorielle de n coûte une comparaison d'entiers, le calcul de la factorielle de n-1 et une multiplication d'entiers Si n = 1, le calcul de la factorielle coûte une comparaison d'entiers 26
27 Factorielle récursive (2/2) On pose une équation de récurrence : appelons c(n) la complexité c(n) = ce + c(n-1) + oe si n 1 c(1) = ce On résoud cette équation de récurrence : c(n) = n*ce + (n-1)*oe = O(n) La complexité de la factorielle récursive est donc linéaire, comme celle de la factorielle itérative. A l'exécution, la fonction récursive est un peu moins rapide (pente de la droite plus forte) du fait des appels récursifs. 27
28 Complexité et récursivité En général, dérécursiver un algorithme ne change pas la forme de sa complexité, pas plus que passer en récursivité terminale! Il existe diverses techniques pour la résolution des équations de récurrence (méthode des fonctions génératrices et décomposition des fractions rationnelles, transformée en Z, ). Théorème : soit T(n) une fonction définie par l'équation de récurrence suivante, où b 2, k 0, a > 0, c > 0 et d >0 : T(n) = a*t(n/b) + c*n k si a > b k alors T(n) Θ (n logb(a) ) si a = b k alors T(n) Θ (n k *log(n)) si a < b k alors T(n) Θ n k 28
29 Résolution des récurrences (1/2) Equation : c(n) = c(n-1) + b Solution : c(n) = c(0) + b*n = O(n) Exemples : factorielle, recherche séquentielle récursive dans un tableau Equation : c(n) = a*c(n-1) + b, a 1 Solution : c(n) = a n *(c(0) b/(1-a)) + b/(1-a) = O(a n ) Exemples : répétition a fois d'un traitement sur le résultat de l'appel récursif Equation : c(n) = c(n-1) + a*n + b Solution : c(n) = c(0) + a*n*(n+1)/2 + n*b = O(n 2 ). Exemples : traitement en coût linéaire avant l'appel récursif, tri à bulle Equation : c(n) = c(n/2) + b Solution : c(n) = c(1) + b*log 2 (n) = O(log(n)) Exemples : élimination de la moitié des éléments en temps constant avant l'appel récursif, recherche dichotomique récursive 29
30 Résolution des récurrences (2/2) Equation : c(n) = a*c(n/2) + b, a 1 Solution : c(n) = n log2(a) *(c(1) b/(1-a)) + b/(1-a) = O(n log2(a) ) Exemples : répétition a fois d'un traitement sur le résultat de l'appel récursif dichotomique Equation : c(n) = c(n/2) + a*n +b Solution : c(n) = O(n) Exemples : traitement linéaire avant l'appel récursif dichotomique Equation : c(n) = 2*c(n/2) + a*n + b Solution : c(n) = O(n*log(n)) Exemples : traitement linéaire avant double appel récursif dichotomique, tri fusion 30
31 Le piège de Fibonacci (1/2) fonction avec retour entier fibo(entier n) début si ((n = 0) OU (n = 1)) alors retourne 1; sinon retourne fibo(n-1) + fibo(n-2); finsi fin Paramètre de complexité : la valeur de n Un seul cas d'exécution La complexité c(n) vérifie l'équation : c(n) = a + c(n-1) + c(n-2) si n>1 c(1) = 1 c(0) = 1 Solution de l'équation : c(n) = Θ (Φ n ) où Φ = (1+ 5)/2 31
32 Le piège de Fibonacci (2/2) fonction avec retour entier fibo(entier n) entier a, b, c, i; début si ((n = 0) ou (n = 1)) alors retourne 1; sinon a <- 1; b <- 1; pour (i allant de 2 à n pas 1) faire c <- b; b <- a + b; a <- c; finpour retourne b; finsi fin Paramètre de complexité : la valeur de n Un seul cas d'exécution Pour n 0, il y a (n-1) tours de boucles, donc la complexité vaut a*(n-1)+b avec a et b constantes donc la complexité est en O(n). 32
33 Complexité du tri à bulle fonction sans retour tribulle(entier[] tab){ entier i,j,temp; début pour (i allant de tab.longueur-2 à 1 pas -1) faire pour (j allant de 0 à i pas 1) faire si (tab[j] > tab[j+1]) alors temp <- tab[j]; tab[j] <- tab[j+1]; tab[j+1] <- temp; finsi finpour finpour fin Paramètre de complexité : la taille du tableau Cas au pire : les éléments sont triés dans l'ordre inverse de celui voulu Complexité au pire : remonter le premier élément nécessite (n-1) tours de la boucle imbriquée, remonter le deuxième nécessite (n-2) tours, etc. Donc le nombre de tours total est (n-1) + (n-2) = n*(n-1)/2 soit O(n 2 ). Remarque : les tris par sélection et par insertion sont aussi quadratiques. Mais il existe des algorithmes de tri quasi-linéaires. 33
ALGORITHMIQUE II NOTION DE COMPLEXITE. SMI AlgoII
 ALGORITHMIQUE II NOTION DE COMPLEXITE 1 2 Comment choisir entre différents algorithmes pour résoudre un même problème? Plusieurs critères de choix : Exactitude Simplicité Efficacité (but de ce chapitre)
ALGORITHMIQUE II NOTION DE COMPLEXITE 1 2 Comment choisir entre différents algorithmes pour résoudre un même problème? Plusieurs critères de choix : Exactitude Simplicité Efficacité (but de ce chapitre)
Rappels sur les suites - Algorithme
 DERNIÈRE IMPRESSION LE 14 septembre 2015 à 12:36 Rappels sur les suites - Algorithme Table des matières 1 Suite : généralités 2 1.1 Déition................................. 2 1.2 Exemples de suites............................
DERNIÈRE IMPRESSION LE 14 septembre 2015 à 12:36 Rappels sur les suites - Algorithme Table des matières 1 Suite : généralités 2 1.1 Déition................................. 2 1.2 Exemples de suites............................
Recherche dans un tableau
 Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
Chapitre 3 Recherche dans un tableau 3.1 Introduction 3.1.1 Tranche On appelle tranche de tableau, la donnée d'un tableau t et de deux indices a et b. On note cette tranche t.(a..b). Exemple 3.1 : 3 6
1 de 46. Algorithmique. Trouver et Trier. Florent Hivert. Mél : Florent.Hivert@lri.fr Page personnelle : http://www.lri.fr/ hivert
 1 de 46 Algorithmique Trouver et Trier Florent Hivert Mél : Florent.Hivert@lri.fr Page personnelle : http://www.lri.fr/ hivert 2 de 46 Algorithmes et structures de données La plupart des bons algorithmes
1 de 46 Algorithmique Trouver et Trier Florent Hivert Mél : Florent.Hivert@lri.fr Page personnelle : http://www.lri.fr/ hivert 2 de 46 Algorithmes et structures de données La plupart des bons algorithmes
4. Les structures de données statiques
 4. Les structures de données statiques 4.1 Tableaux à une dimension 4.1.1 Introduction Imaginons que dans un programme, nous ayons besoin simultanément de 25 valeurs (par exemple, des notes pour calculer
4. Les structures de données statiques 4.1 Tableaux à une dimension 4.1.1 Introduction Imaginons que dans un programme, nous ayons besoin simultanément de 25 valeurs (par exemple, des notes pour calculer
1 Recherche en table par balayage
 1 Recherche en table par balayage 1.1 Problème de la recherche en table Une table désigne une liste ou un tableau d éléments. Le problème de la recherche en table est celui de la recherche d un élément
1 Recherche en table par balayage 1.1 Problème de la recherche en table Une table désigne une liste ou un tableau d éléments. Le problème de la recherche en table est celui de la recherche d un élément
Chapitre 7. Récurrences
 Chapitre 7 Récurrences 333 Plan 1. Introduction 2. Applications 3. Classification des récurrences 4. Résolution de récurrences 5. Résumé et comparaisons Lectures conseillées : I MCS, chapitre 20. I Rosen,
Chapitre 7 Récurrences 333 Plan 1. Introduction 2. Applications 3. Classification des récurrences 4. Résolution de récurrences 5. Résumé et comparaisons Lectures conseillées : I MCS, chapitre 20. I Rosen,
Architecture des Systèmes d Information Architecture des Systèmes d Information
 Plan... Tableaux et tris I3 - Algorithmique et programmation 1 Rappels Nicol Delestre 2 Tableaux à n dimensions 3 Initiation aux tris Tableaux - v2.0.1 1 / 27 Tableaux - v2.0.1 2 / 27 Rappels : tableau
Plan... Tableaux et tris I3 - Algorithmique et programmation 1 Rappels Nicol Delestre 2 Tableaux à n dimensions 3 Initiation aux tris Tableaux - v2.0.1 1 / 27 Tableaux - v2.0.1 2 / 27 Rappels : tableau
Calculateur quantique: factorisation des entiers
 Calculateur quantique: factorisation des entiers Plan Introduction Difficulté de la factorisation des entiers Cryptographie et la factorisation Exemple RSA L'informatique quantique L'algorithme quantique
Calculateur quantique: factorisation des entiers Plan Introduction Difficulté de la factorisation des entiers Cryptographie et la factorisation Exemple RSA L'informatique quantique L'algorithme quantique
Algorithme. Table des matières
 1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
1 Algorithme Table des matières 1 Codage 2 1.1 Système binaire.............................. 2 1.2 La numérotation de position en base décimale............ 2 1.3 La numérotation de position en base binaire..............
Cours d introduction à l informatique. Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions
 Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d introduction à l informatique Partie 2 : Comment écrire un algorithme? Qu est-ce qu une variable? Expressions et instructions Qu est-ce qu un Une recette de cuisine algorithme? Protocole expérimental
Cours d Informatique
 Cours d Informatique 1ère année SM/SMI 2007/2008, Info 2 Département de Mathématiques et d Informatique, Université Mohammed V elbenani@hotmail.com sayah@fsr.ac.ma 2007/2008 Info2, 1ère année SM/SMI 1
Cours d Informatique 1ère année SM/SMI 2007/2008, Info 2 Département de Mathématiques et d Informatique, Université Mohammed V elbenani@hotmail.com sayah@fsr.ac.ma 2007/2008 Info2, 1ère année SM/SMI 1
LE PROBLEME DU PLUS COURT CHEMIN
 LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
LE PROBLEME DU PLUS COURT CHEMIN Dans cette leçon nous définissons le modèle de plus court chemin, présentons des exemples d'application et proposons un algorithme de résolution dans le cas où les longueurs
Algorithmes récursifs
 Licence 1 MASS - Algorithmique et Calcul Formel S. Verel, M.-E. Voge www.i3s.unice.fr/ verel 23 mars 2007 Objectifs de la séance 3 écrire des algorithmes récursifs avec un seul test rechercher un élément
Licence 1 MASS - Algorithmique et Calcul Formel S. Verel, M.-E. Voge www.i3s.unice.fr/ verel 23 mars 2007 Objectifs de la séance 3 écrire des algorithmes récursifs avec un seul test rechercher un élément
Corrigé des TD 1 à 5
 Corrigé des TD 1 à 5 1 Premier Contact 1.1 Somme des n premiers entiers 1 (* Somme des n premiers entiers *) 2 program somme_entiers; n, i, somme: integer; 8 (* saisie du nombre n *) write( Saisissez un
Corrigé des TD 1 à 5 1 Premier Contact 1.1 Somme des n premiers entiers 1 (* Somme des n premiers entiers *) 2 program somme_entiers; n, i, somme: integer; 8 (* saisie du nombre n *) write( Saisissez un
Programmation C++ (débutant)/instructions for, while et do...while
 Programmation C++ (débutant)/instructions for, while et do...while 1 Programmation C++ (débutant)/instructions for, while et do...while Le cours du chapitre 4 : le for, while et do...while La notion de
Programmation C++ (débutant)/instructions for, while et do...while 1 Programmation C++ (débutant)/instructions for, while et do...while Le cours du chapitre 4 : le for, while et do...while La notion de
UEO11 COURS/TD 1. nombres entiers et réels codés en mémoire centrale. Caractères alphabétiques et caractères spéciaux.
 UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
UEO11 COURS/TD 1 Contenu du semestre Cours et TDs sont intégrés L objectif de ce cours équivalent a 6h de cours, 10h de TD et 8h de TP est le suivant : - initiation à l algorithmique - notions de bases
Programmation Objet - Cours II
 Programmation Objet - Cours II - Exercices - Page 1 Programmation Objet - Cours II Exercices Auteur : E.Thirion - Dernière mise à jour : 05/07/2015 Les exercices suivants sont en majorité des projets à
Programmation Objet - Cours II - Exercices - Page 1 Programmation Objet - Cours II Exercices Auteur : E.Thirion - Dernière mise à jour : 05/07/2015 Les exercices suivants sont en majorité des projets à
 Licence ST Université Claude Bernard Lyon I LIF1 : Algorithmique et Programmation C Bases du langage C 1 Conclusion de la dernière fois Introduction de l algorithmique générale pour permettre de traiter
Licence ST Université Claude Bernard Lyon I LIF1 : Algorithmique et Programmation C Bases du langage C 1 Conclusion de la dernière fois Introduction de l algorithmique générale pour permettre de traiter
Algorithmique avec Algobox
 Algorithmique avec Algobox Fiche 2 Cette fiche est la suite directe de la première. 1. Instructions conditionnelles : 1.1. Reprise de la fiche 1 : Lecture d'un algorithme : ORDINATEUR INTERDIT : Après
Algorithmique avec Algobox Fiche 2 Cette fiche est la suite directe de la première. 1. Instructions conditionnelles : 1.1. Reprise de la fiche 1 : Lecture d'un algorithme : ORDINATEUR INTERDIT : Après
Initiation à l algorithmique
 Informatique S1 Initiation à l algorithmique procédures et fonctions 2. Appel d une fonction Jacques TISSEAU Ecole Nationale d Ingénieurs de Brest Technopôle Brest-Iroise CS 73862-29238 Brest cedex 3 -
Informatique S1 Initiation à l algorithmique procédures et fonctions 2. Appel d une fonction Jacques TISSEAU Ecole Nationale d Ingénieurs de Brest Technopôle Brest-Iroise CS 73862-29238 Brest cedex 3 -
CCP PSI - 2010 Mathématiques 1 : un corrigé
 CCP PSI - 00 Mathématiques : un corrigé Première partie. Définition d une structure euclidienne sur R n [X]... B est clairement symétrique et linéaire par rapport à sa seconde variable. De plus B(P, P
CCP PSI - 00 Mathématiques : un corrigé Première partie. Définition d une structure euclidienne sur R n [X]... B est clairement symétrique et linéaire par rapport à sa seconde variable. De plus B(P, P
Raisonnement par récurrence Suites numériques
 Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Chapitre 1 Raisonnement par récurrence Suites numériques Terminale S Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Raisonnement par récurrence. Limite finie ou infinie d une suite.
Correction TD algorithmique
 Affectation Correction TD algorithmique Exercice 1 algo affect1b b 5 a b+1 b 2 Il vaut faire passer la notion de variable et la notion de stockage mémoire. Une variable n a donc pas d historique et à un
Affectation Correction TD algorithmique Exercice 1 algo affect1b b 5 a b+1 b 2 Il vaut faire passer la notion de variable et la notion de stockage mémoire. Une variable n a donc pas d historique et à un
Algorithmique avec Algobox
 Algorithmique avec Algobox 1. Algorithme: Un algorithme est une suite d instructions qui, une fois exécutée correctement, conduit à un résultat donné Un algorithme doit contenir uniquement des instructions
Algorithmique avec Algobox 1. Algorithme: Un algorithme est une suite d instructions qui, une fois exécutée correctement, conduit à un résultat donné Un algorithme doit contenir uniquement des instructions
CORRECTION EXERCICES ALGORITHME 1
 CORRECTION 1 Mr KHATORY (GIM 1 A) 1 Ecrire un algorithme permettant de résoudre une équation du second degré. Afficher les solutions! 2 2 b b 4ac ax bx c 0; solution: x 2a Solution: ALGORITHME seconddegré
CORRECTION 1 Mr KHATORY (GIM 1 A) 1 Ecrire un algorithme permettant de résoudre une équation du second degré. Afficher les solutions! 2 2 b b 4ac ax bx c 0; solution: x 2a Solution: ALGORITHME seconddegré
d algorithmique D. Beauquier, J. Berstel, Ph. Chrétienne
 Éléments d algorithmique D. Beauquier, J. Berstel, Ph. Chrétienne 6 février 005 c D. Beauquier, J. Berstel, Ph. Chrétienne, 003 Première édition par Masson, 99. 3 à Bruno Sophie Bruno Clara Jérôme Solange
Éléments d algorithmique D. Beauquier, J. Berstel, Ph. Chrétienne 6 février 005 c D. Beauquier, J. Berstel, Ph. Chrétienne, 003 Première édition par Masson, 99. 3 à Bruno Sophie Bruno Clara Jérôme Solange
Table des matières. I Mise à niveau 11. Préface
 Table des matières Préface v I Mise à niveau 11 1 Bases du calcul commercial 13 1.1 Alphabet grec...................................... 13 1.2 Symboles mathématiques............................... 14 1.3
Table des matières Préface v I Mise à niveau 11 1 Bases du calcul commercial 13 1.1 Alphabet grec...................................... 13 1.2 Symboles mathématiques............................... 14 1.3
Bases de programmation. Cours 5. Structurer les données
 Bases de programmation. Cours 5. Structurer les données Pierre Boudes 1 er décembre 2014 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License. Types char et
Bases de programmation. Cours 5. Structurer les données Pierre Boudes 1 er décembre 2014 This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License. Types char et
Initiation à la programmation en Python
 I-Conventions Initiation à la programmation en Python Nom : Prénom : Une commande Python sera écrite en caractère gras. Exemples : print 'Bonjour' max=input("nombre maximum autorisé :") Le résultat de
I-Conventions Initiation à la programmation en Python Nom : Prénom : Une commande Python sera écrite en caractère gras. Exemples : print 'Bonjour' max=input("nombre maximum autorisé :") Le résultat de
La fonction exponentielle
 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2. Définition et théorèmes.......................... 2.2 Approche graphique de la fonction
ELEC2753 Electrotechnique examen du 11/06/2012
 ELEC2753 Electrotechnique examen du 11/06/2012 Pour faciliter la correction et la surveillance, merci de répondre aux 3 questions sur des feuilles différentes et d'écrire immédiatement votre nom sur toutes
ELEC2753 Electrotechnique examen du 11/06/2012 Pour faciliter la correction et la surveillance, merci de répondre aux 3 questions sur des feuilles différentes et d'écrire immédiatement votre nom sur toutes
Représentation d un entier en base b
 Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Représentation d un entier en base b 13 octobre 2012 1 Prérequis Les bases de la programmation en langage sont supposées avoir été travaillées L écriture en base b d un entier est ainsi défini à partir
Chapitre 3. Quelques fonctions usuelles. 1 Fonctions logarithme et exponentielle. 1.1 La fonction logarithme
 Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
Chapitre 3 Quelques fonctions usuelles 1 Fonctions logarithme et eponentielle 1.1 La fonction logarithme Définition 1.1 La fonction 7! 1/ est continue sur ]0, +1[. Elle admet donc des primitives sur cet
MISE A NIVEAU INFORMATIQUE LANGAGE C - EXEMPLES DE PROGRAMMES. Université Paris Dauphine IUP Génie Mathématique et Informatique 2 ème année
 2003-2004 Université Paris Dauphine IUP Génie Mathématique et Informatique 2 ème année MISE A NIVEAU INFORMATIQUE LANGAGE C - EXEMPLES DE PROGRAMMES Maude Manouvrier La reproduction de ce document par
2003-2004 Université Paris Dauphine IUP Génie Mathématique et Informatique 2 ème année MISE A NIVEAU INFORMATIQUE LANGAGE C - EXEMPLES DE PROGRAMMES Maude Manouvrier La reproduction de ce document par
1/24. I passer d un problème exprimé en français à la réalisation d un. I expressions arithmétiques. I structures de contrôle (tests, boucles)
 1/4 Objectif de ce cours /4 Objectifs de ce cours Introduction au langage C - Cours Girardot/Roelens Septembre 013 Du problème au programme I passer d un problème exprimé en français à la réalisation d
1/4 Objectif de ce cours /4 Objectifs de ce cours Introduction au langage C - Cours Girardot/Roelens Septembre 013 Du problème au programme I passer d un problème exprimé en français à la réalisation d
Résolution de systèmes linéaires par des méthodes directes
 Résolution de systèmes linéaires par des méthodes directes J. Erhel Janvier 2014 1 Inverse d une matrice carrée et systèmes linéaires Ce paragraphe a pour objet les matrices carrées et les systèmes linéaires.
Résolution de systèmes linéaires par des méthodes directes J. Erhel Janvier 2014 1 Inverse d une matrice carrée et systèmes linéaires Ce paragraphe a pour objet les matrices carrées et les systèmes linéaires.
Travaux pratiques. Compression en codage de Huffman. 1.3. Organisation d un projet de programmation
 Université de Savoie Module ETRS711 Travaux pratiques Compression en codage de Huffman 1. Organisation du projet 1.1. Objectifs Le but de ce projet est d'écrire un programme permettant de compresser des
Université de Savoie Module ETRS711 Travaux pratiques Compression en codage de Huffman 1. Organisation du projet 1.1. Objectifs Le but de ce projet est d'écrire un programme permettant de compresser des
Organigramme / Algorigramme Dossier élève 1 SI
 Organigramme / Algorigramme Dossier élève 1 SI CI 10, I11 ; CI 11, I10 C24 Algorithmique 8 février 2009 (13:47) 1. Introduction Un organigramme (ou algorigramme, lorsqu il est plus particulièrement appliqué
Organigramme / Algorigramme Dossier élève 1 SI CI 10, I11 ; CI 11, I10 C24 Algorithmique 8 février 2009 (13:47) 1. Introduction Un organigramme (ou algorigramme, lorsqu il est plus particulièrement appliqué
Chapitre 4: Dérivée d'une fonction et règles de calcul
 DERIVEES ET REGLES DE CALCULS 69 Chapitre 4: Dérivée d'une fonction et règles de calcul Prérequis: Généralités sur les fonctions, Introduction dérivée Requis pour: Croissance, Optimisation, Études de fct.
DERIVEES ET REGLES DE CALCULS 69 Chapitre 4: Dérivée d'une fonction et règles de calcul Prérequis: Généralités sur les fonctions, Introduction dérivée Requis pour: Croissance, Optimisation, Études de fct.
Chapitre 1 Régime transitoire dans les systèmes physiques
 Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer
Chapitre 1 Régime transitoire dans les systèmes physiques Savoir-faire théoriques (T) : Écrire l équation différentielle associée à un système physique ; Faire apparaître la constante de temps ; Tracer
Développements limités. Notion de développement limité
 MT12 - ch2 Page 1/8 Développements limités Dans tout ce chapitre, I désigne un intervalle de R non vide et non réduit à un point. I Notion de développement limité Dans tout ce paragraphe, a désigne un
MT12 - ch2 Page 1/8 Développements limités Dans tout ce chapitre, I désigne un intervalle de R non vide et non réduit à un point. I Notion de développement limité Dans tout ce paragraphe, a désigne un
Souad EL Bernoussi. Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/
 Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Recherche opérationnelle Les démonstrations et les exemples seront traités en cours Souad EL Bernoussi Groupe d Analyse Numérique et Optimisation Rabat http ://www.fsr.ac.ma/ano/ Table des matières 1 Programmation
Cours d Algorithmique et de Langage C 2005 - v 3.0
 Cours d Algorithmique et de Langage C 2005 - v 3.0 Bob CORDEAU cordeau@onera.fr Mesures Physiques IUT d Orsay 15 mai 2006 Avant-propos Avant-propos Ce cours en libre accès repose sur trois partis pris
Cours d Algorithmique et de Langage C 2005 - v 3.0 Bob CORDEAU cordeau@onera.fr Mesures Physiques IUT d Orsay 15 mai 2006 Avant-propos Avant-propos Ce cours en libre accès repose sur trois partis pris
Algorithmique et Programmation, IMA
 Algorithmique et Programmation, IMA Cours 2 : C Premier Niveau / Algorithmique Université Lille 1 - Polytech Lille Notations, identificateurs Variables et Types de base Expressions Constantes Instructions
Algorithmique et Programmation, IMA Cours 2 : C Premier Niveau / Algorithmique Université Lille 1 - Polytech Lille Notations, identificateurs Variables et Types de base Expressions Constantes Instructions
Définitions. Numéro à préciser. (Durée : )
 Numéro à préciser (Durée : ) On étudie dans ce problème l ordre lexicographique pour les mots sur un alphabet fini et plusieurs constructions des cycles de De Bruijn. Les trois parties sont largement indépendantes.
Numéro à préciser (Durée : ) On étudie dans ce problème l ordre lexicographique pour les mots sur un alphabet fini et plusieurs constructions des cycles de De Bruijn. Les trois parties sont largement indépendantes.
SUPPORT DE COURS. Dr. Omari Mohammed Maître de Conférences Classe A Université d Adrar Courriel : omarinmt@gmail.com
 Dr. Omari Mohammed Maître de Conférences Classe A Université d Adrar Courriel : omarinmt@gmail.com SUPPORT DE COURS Matière : Algorithmiques et Structures de Données 1 Niveau : 2 ème Année Licence en Informatique
Dr. Omari Mohammed Maître de Conférences Classe A Université d Adrar Courriel : omarinmt@gmail.com SUPPORT DE COURS Matière : Algorithmiques et Structures de Données 1 Niveau : 2 ème Année Licence en Informatique
Cours Informatique Master STEP
 Cours Informatique Master STEP Bases de la programmation: Compilateurs/logiciels Algorithmique et structure d'un programme Programmation en langage structuré (Fortran 90) Variables, expressions, instructions
Cours Informatique Master STEP Bases de la programmation: Compilateurs/logiciels Algorithmique et structure d'un programme Programmation en langage structuré (Fortran 90) Variables, expressions, instructions
Feuille TD n 1 Exercices d algorithmique éléments de correction
 Master Sciences, Technologies, Santé Mention Mathématiques, spécialité Enseignement des mathématiques Algorithmique et graphes, thèmes du second degré Feuille TD n 1 Exercices d algorithmique éléments
Master Sciences, Technologies, Santé Mention Mathématiques, spécialité Enseignement des mathématiques Algorithmique et graphes, thèmes du second degré Feuille TD n 1 Exercices d algorithmique éléments
PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES
 Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Leçon 11 PROBLEMES D'ORDONNANCEMENT AVEC RESSOURCES Dans cette leçon, nous retrouvons le problème d ordonnancement déjà vu mais en ajoutant la prise en compte de contraintes portant sur les ressources.
Programmes des classes préparatoires aux Grandes Ecoles
 Programmes des classes préparatoires aux Grandes Ecoles Filière : scientifique Voies : Mathématiques, physique et sciences de l'ingénieur (MPSI) Physique, chimie et sciences de l ingénieur (PCSI) Physique,
Programmes des classes préparatoires aux Grandes Ecoles Filière : scientifique Voies : Mathématiques, physique et sciences de l'ingénieur (MPSI) Physique, chimie et sciences de l ingénieur (PCSI) Physique,
3 Approximation de solutions d équations
 3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
3 Approximation de solutions d équations Une équation scalaire a la forme générale f(x) =0où f est une fonction de IR dans IR. Un système de n équations à n inconnues peut aussi se mettre sous une telle
Centre CPGE TSI - Safi 2010/2011. Algorithmique et programmation :
 Algorithmique et programmation : STRUCTURES DE DONNÉES A. Structure et enregistrement 1) Définition et rôle des structures de données en programmation 1.1) Définition : En informatique, une structure de
Algorithmique et programmation : STRUCTURES DE DONNÉES A. Structure et enregistrement 1) Définition et rôle des structures de données en programmation 1.1) Définition : En informatique, une structure de
Adama MBODJI MBODJ.SYSTEM
 MBODJ.SYSTEM Tableaux & vecteurs Algorithmes de tris Chaînes de caractères Listes linéaires Piles & Files Arbres Fichiers Je dédie cet ouvrage à mon père Souleymane MBODJI 2 Dédicace... 2 Sommaire... 3
MBODJ.SYSTEM Tableaux & vecteurs Algorithmes de tris Chaînes de caractères Listes linéaires Piles & Files Arbres Fichiers Je dédie cet ouvrage à mon père Souleymane MBODJI 2 Dédicace... 2 Sommaire... 3
Exercices - Polynômes : corrigé. Opérations sur les polynômes
 Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Opérations sur les polynômes Exercice 1 - Carré - L1/Math Sup - Si P = Q est le carré d un polynôme, alors Q est nécessairement de degré, et son coefficient dominant est égal à 1. On peut donc écrire Q(X)
Licence Sciences et Technologies Examen janvier 2010
 Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
Université de Provence Introduction à l Informatique Licence Sciences et Technologies Examen janvier 2010 Année 2009-10 Aucun document n est autorisé Les exercices peuvent être traités dans le désordre.
Algorithmique et structures de données I
 Algorithmique et structures de données I Riadh Ben Messaoud Université 7 novembre à Carthage Faculté des Sciences Économiques et de Gestion de Nabeul 1ère année Licence Fondamentale IAG 1ère année Licence
Algorithmique et structures de données I Riadh Ben Messaoud Université 7 novembre à Carthage Faculté des Sciences Économiques et de Gestion de Nabeul 1ère année Licence Fondamentale IAG 1ère année Licence
Algorithmique, graphes et programmation dynamique Notes de Cours Rapport de Travaux Pratiques. Laurent Canet
 Algorithmique, graphes et programmation dynamique Notes de Cours Rapport de Travaux Pratiques Laurent Canet Le 2 juillet 2003 Table des matières I IN202 - Algorithmique 6 1 Système formel de preuve de
Algorithmique, graphes et programmation dynamique Notes de Cours Rapport de Travaux Pratiques Laurent Canet Le 2 juillet 2003 Table des matières I IN202 - Algorithmique 6 1 Système formel de preuve de
Limitations of the Playstation 3 for High Performance Cluster Computing
 Introduction Plan Limitations of the Playstation 3 for High Performance Cluster Computing July 2007 Introduction Plan Introduction Intérêts de la PS3 : rapide et puissante bon marché L utiliser pour faire
Introduction Plan Limitations of the Playstation 3 for High Performance Cluster Computing July 2007 Introduction Plan Introduction Intérêts de la PS3 : rapide et puissante bon marché L utiliser pour faire
Algorithmes et Programmes. Introduction à l informatiquel. Cycle de vie d'un programme (d'un logiciel) Cycle de vie d'un programme (d'un logiciel)
 Algorithmes et Programmes Introduction à l informatiquel! Vie d'un programme! Algorithme! Programmation : le langage! Exécution et test des programmes Chapitre : Algorithmes et Programmes 2 Cycle de vie
Algorithmes et Programmes Introduction à l informatiquel! Vie d'un programme! Algorithme! Programmation : le langage! Exécution et test des programmes Chapitre : Algorithmes et Programmes 2 Cycle de vie
TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile
 TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile Dans ce TP, vous apprendrez à définir le type abstrait Pile, à le programmer en Java à l aide d une interface
TP n 2 Concepts de la programmation Objets Master 1 mention IL, semestre 2 Le type Abstrait Pile Dans ce TP, vous apprendrez à définir le type abstrait Pile, à le programmer en Java à l aide d une interface
Algorithmes de recherche
 Algorithmes de recherche 1 Résolution de problèmes par recherche On représente un problème par un espace d'états (arbre/graphe). Chaque état est une conguration possible du problème. Résoudre le problème
Algorithmes de recherche 1 Résolution de problèmes par recherche On représente un problème par un espace d'états (arbre/graphe). Chaque état est une conguration possible du problème. Résoudre le problème
CHAPITRE VIII : Les circuits avec résistances ohmiques
 CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
CHAPITRE VIII : Les circuits avec résistances ohmiques VIII. 1 Ce chapitre porte sur les courants et les différences de potentiel dans les circuits. VIII.1 : Les résistances en série et en parallèle On
Maple: premiers calculs et premières applications
 TP Maple: premiers calculs et premières applications Maple: un logiciel de calcul formel Le logiciel Maple est un système de calcul formel. Alors que la plupart des logiciels de mathématiques utilisent
TP Maple: premiers calculs et premières applications Maple: un logiciel de calcul formel Le logiciel Maple est un système de calcul formel. Alors que la plupart des logiciels de mathématiques utilisent
Résolution d équations non linéaires
 Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Analyse Numérique Résolution d équations non linéaires Said EL HAJJI et Touria GHEMIRES Université Mohammed V - Agdal. Faculté des Sciences Département de Mathématiques. Laboratoire de Mathématiques, Informatique
Une réponse (très) partielle à la deuxième question : Calcul des exposants critiques en champ moyen
 Une réponse (très) partielle à la deuxième question : Calcul des exposants critiques en champ moyen Manière heuristique d'introduire l'approximation de champ moyen : on néglige les termes de fluctuations
Une réponse (très) partielle à la deuxième question : Calcul des exposants critiques en champ moyen Manière heuristique d'introduire l'approximation de champ moyen : on néglige les termes de fluctuations
Polynômes à plusieurs variables. Résultant
 Polynômes à plusieurs variables. Résultant Christophe Ritzenthaler 1 Relations coefficients-racines. Polynômes symétriques Issu de [MS] et de [Goz]. Soit A un anneau intègre. Définition 1.1. Soit a A \
Polynômes à plusieurs variables. Résultant Christophe Ritzenthaler 1 Relations coefficients-racines. Polynômes symétriques Issu de [MS] et de [Goz]. Soit A un anneau intègre. Définition 1.1. Soit a A \
Sub CalculAnnuite() Const TITRE As String = "Calcul d'annuité de remboursement d'un emprunt"
 TD1 : traduction en Visual BASIC des exemples du cours sur les structures de contrôle de l'exécution page 1 'TRADUCTION EN VBA DES EXEMPLES ALGORITHMIQUES SUR LES STRUCTURES 'DE CONTROLE DE L'EXECUTION
TD1 : traduction en Visual BASIC des exemples du cours sur les structures de contrôle de l'exécution page 1 'TRADUCTION EN VBA DES EXEMPLES ALGORITHMIQUES SUR LES STRUCTURES 'DE CONTROLE DE L'EXECUTION
Leçon 01 Exercices d'entraînement
 Leçon 01 Exercices d'entraînement Exercice 1 Etudier la convergence des suites ci-dessous définies par leur terme général: 1)u n = 2n3-5n + 1 n 2 + 3 2)u n = 2n2-7n - 5 -n 5-1 4)u n = lnn2 n+1 5)u n =
Leçon 01 Exercices d'entraînement Exercice 1 Etudier la convergence des suites ci-dessous définies par leur terme général: 1)u n = 2n3-5n + 1 n 2 + 3 2)u n = 2n2-7n - 5 -n 5-1 4)u n = lnn2 n+1 5)u n =
Problème : Calcul d'échéanciers de prêt bancaire (15 pt)
 Problème : Calcul d'échéanciers de prêt bancaire (15 pt) 1 Principe d'un prêt bancaire et dénitions Lorsque vous empruntez de l'argent dans une banque, cet argent (appelé capital) vous est loué. Chaque
Problème : Calcul d'échéanciers de prêt bancaire (15 pt) 1 Principe d'un prêt bancaire et dénitions Lorsque vous empruntez de l'argent dans une banque, cet argent (appelé capital) vous est loué. Chaque
Suites numériques 4. 1 Autres recettes pour calculer les limites
 Suites numériques 4 1 Autres recettes pour calculer les limites La propriété suivante permet de calculer certaines limites comme on verra dans les exemples qui suivent. Propriété 1. Si u n l et fx) est
Suites numériques 4 1 Autres recettes pour calculer les limites La propriété suivante permet de calculer certaines limites comme on verra dans les exemples qui suivent. Propriété 1. Si u n l et fx) est
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT
 Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
Exercices types Algorithmique et simulation numérique Oral Mathématiques et algorithmique Banque PT Ces exercices portent sur les items 2, 3 et 5 du programme d informatique des classes préparatoires,
L exclusion mutuelle distribuée
 L exclusion mutuelle distribuée L algorithme de L Amport L algorithme est basé sur 2 concepts : L estampillage des messages La distribution d une file d attente sur l ensemble des sites du système distribué
L exclusion mutuelle distribuée L algorithme de L Amport L algorithme est basé sur 2 concepts : L estampillage des messages La distribution d une file d attente sur l ensemble des sites du système distribué
LES NOMBRES DECIMAUX. I. Les programmes
 LES NOMBRES DECIMAUX I. Les programmes Au cycle des approfondissements (Cours Moyen), une toute première approche des fractions est entreprise, dans le but d aider à la compréhension des nombres décimaux.
LES NOMBRES DECIMAUX I. Les programmes Au cycle des approfondissements (Cours Moyen), une toute première approche des fractions est entreprise, dans le but d aider à la compréhension des nombres décimaux.
Quelques Algorithmes simples
 Quelques Algorithmes simples Irène Guessarian ig@liafa.jussieu.fr 10 janvier 2012 Je remercie Patrick Cegielski de son aide efficace pour la programmation Java ; la section sur le codage de Huffman a été
Quelques Algorithmes simples Irène Guessarian ig@liafa.jussieu.fr 10 janvier 2012 Je remercie Patrick Cegielski de son aide efficace pour la programmation Java ; la section sur le codage de Huffman a été
introduction Chapitre 5 Récursivité Exemples mathématiques Fonction factorielle ø est un arbre (vide) Images récursives
 introduction Chapitre 5 Images récursives http ://univ-tln.fr/~papini/sources/flocon.htm Récursivité http://www.poulain.org/fractales/index.html Image qui se contient elle-même 1 Exemples mathématiques
introduction Chapitre 5 Images récursives http ://univ-tln.fr/~papini/sources/flocon.htm Récursivité http://www.poulain.org/fractales/index.html Image qui se contient elle-même 1 Exemples mathématiques
Chp. 4. Minimisation d une fonction d une variable
 Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Chp. 4. Minimisation d une fonction d une variable Avertissement! Dans tout ce chapître, I désigne un intervalle de IR. 4.1 Fonctions convexes d une variable Définition 9 Une fonction ϕ, partout définie
Ordonnancement. N: nains de jardin. X: peinture extérieure. E: électricité T: toit. M: murs. F: fondations CHAPTER 1
 CHAPTER 1 Ordonnancement 1.1. Étude de cas Ordonnancement de tâches avec contraintes de précédences 1.1.1. Exemple : construction d'une maison. Exercice. On veut construire une maison, ce qui consiste
CHAPTER 1 Ordonnancement 1.1. Étude de cas Ordonnancement de tâches avec contraintes de précédences 1.1.1. Exemple : construction d'une maison. Exercice. On veut construire une maison, ce qui consiste
Grandes lignes ASTRÉE. Logiciels critiques. Outils de certification classiques. Inspection manuelle. Definition. Test
 Grandes lignes Analyseur Statique de logiciels Temps RÉel Embarqués École Polytechnique École Normale Supérieure Mercredi 18 juillet 2005 1 Présentation d 2 Cadre théorique de l interprétation abstraite
Grandes lignes Analyseur Statique de logiciels Temps RÉel Embarqués École Polytechnique École Normale Supérieure Mercredi 18 juillet 2005 1 Présentation d 2 Cadre théorique de l interprétation abstraite
Notes du cours MTH1101 Calcul I Partie II: fonctions de plusieurs variables
 Notes du cours MTH1101 Calcul I Partie II: fonctions de plusieurs variables Guy Desaulniers Département de mathématiques et de génie industriel École Polytechnique de Montréal Automne 2014 Table des matières
Notes du cours MTH1101 Calcul I Partie II: fonctions de plusieurs variables Guy Desaulniers Département de mathématiques et de génie industriel École Polytechnique de Montréal Automne 2014 Table des matières
INITIATION AU LANGAGE C SUR PIC DE MICROSHIP
 COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
COURS PROGRAMMATION INITIATION AU LANGAGE C SUR MICROCONTROLEUR PIC page 1 / 7 INITIATION AU LANGAGE C SUR PIC DE MICROSHIP I. Historique du langage C 1972 : naissance du C dans les laboratoires BELL par
Sites web éducatifs et ressources en mathématiques
 Sites web éducatifs et ressources en mathématiques Exercices en ligne pour le primaire Calcul mental élémentaire : http://www.csaffluents.qc.ca/wlamen/tables-sous.html Problèmes de soustraction/addition
Sites web éducatifs et ressources en mathématiques Exercices en ligne pour le primaire Calcul mental élémentaire : http://www.csaffluents.qc.ca/wlamen/tables-sous.html Problèmes de soustraction/addition
PROJET ALGORITHMIQUE ET PROGRAMMATION II
 PROJET 1 ALGORITHMIQUE ET PROGRAMMATION II CONTENU DU RAPPORT A RENDRE : o Fiche signalétique du binôme o Listing des différents fichiers sources o CD sources o Il sera tenu compte de la présentation du
PROJET 1 ALGORITHMIQUE ET PROGRAMMATION II CONTENU DU RAPPORT A RENDRE : o Fiche signalétique du binôme o Listing des différents fichiers sources o CD sources o Il sera tenu compte de la présentation du
Série TD 3. Exercice 4.1. Exercice 4.2 Cet algorithme est destiné à prédire l'avenir, et il doit être infaillible! Exercice 4.3. Exercice 4.
 Série TD 3 Exercice 4.1 Formulez un algorithme équivalent à l algorithme suivant : Si Tutu > Toto + 4 OU Tata = OK Alors Tutu Tutu + 1 Tutu Tutu 1 ; Exercice 4.2 Cet algorithme est destiné à prédire l'avenir,
Série TD 3 Exercice 4.1 Formulez un algorithme équivalent à l algorithme suivant : Si Tutu > Toto + 4 OU Tata = OK Alors Tutu Tutu + 1 Tutu Tutu 1 ; Exercice 4.2 Cet algorithme est destiné à prédire l'avenir,
DYNAMIQUE DE FORMATION DES ÉTOILES
 A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
A 99 PHYS. II ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE,
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications
 Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
Optimisation non linéaire Irène Charon, Olivier Hudry École nationale supérieure des télécommunications A. Optimisation sans contrainte.... Généralités.... Condition nécessaire et condition suffisante
Algorithmique et Programmation
 École Supérieure d Ingénieurs de Poitiers Gea Algorithmique et Programmation Laurent Signac ii Algorithmique et programmation Gea Table des matières Avant Propos v Structures de données Notion de pointeur..............................................
École Supérieure d Ingénieurs de Poitiers Gea Algorithmique et Programmation Laurent Signac ii Algorithmique et programmation Gea Table des matières Avant Propos v Structures de données Notion de pointeur..............................................
Rappel. Analyse de Données Structurées - Cours 12. Un langage avec des déclaration locales. Exemple d'un programme
 Rappel Ralf Treinen Université Paris Diderot UFR Informatique Laboratoire Preuves, Programmes et Systèmes treinen@pps.univ-paris-diderot.fr 6 mai 2015 Jusqu'à maintenant : un petit langage de programmation
Rappel Ralf Treinen Université Paris Diderot UFR Informatique Laboratoire Preuves, Programmes et Systèmes treinen@pps.univ-paris-diderot.fr 6 mai 2015 Jusqu'à maintenant : un petit langage de programmation
CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE. Cinquième épreuve d admissibilité STATISTIQUE. (durée : cinq heures)
 CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE Cinquième épreuve d admissibilité STATISTIQUE (durée : cinq heures) Une composition portant sur la statistique. SUJET Cette épreuve est composée d un
CONCOURS D ENTREE A L ECOLE DE 2007 CONCOURS EXTERNE Cinquième épreuve d admissibilité STATISTIQUE (durée : cinq heures) Une composition portant sur la statistique. SUJET Cette épreuve est composée d un
Fonctionnalités d Acronis :
 Sommaire Introduction... 2 Fonctionnalités d Acronis :... 2 Concepts de base d'acronis True Image Home... 3 Version d Acronis... 4 Configuration requise pour Acronis True Image Home 2015... 4 Systèmes
Sommaire Introduction... 2 Fonctionnalités d Acronis :... 2 Concepts de base d'acronis True Image Home... 3 Version d Acronis... 4 Configuration requise pour Acronis True Image Home 2015... 4 Systèmes
STAGE IREM 0- Premiers pas en Python
 Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
Université de Bordeaux 16-18 Février 2014/2015 STAGE IREM 0- Premiers pas en Python IREM de Bordeaux Affectation et expressions Le langage python permet tout d abord de faire des calculs. On peut évaluer
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé.
 Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
Baccalauréat L spécialité, Métropole et Réunion, 19 juin 2009 Corrigé. L usage d une calculatrice est autorisé Durée : 3heures Deux annexes sont à rendre avec la copie. Exercice 1 5 points 1_ Soit f la
IN 102 - Cours 1. 1 Informatique, calculateurs. 2 Un premier programme en C
 IN 102 - Cours 1 Qu on le veuille ou non, les systèmes informatisés sont désormais omniprésents. Même si ne vous destinez pas à l informatique, vous avez de très grandes chances d y être confrontés en
IN 102 - Cours 1 Qu on le veuille ou non, les systèmes informatisés sont désormais omniprésents. Même si ne vous destinez pas à l informatique, vous avez de très grandes chances d y être confrontés en
Probabilités. Rappel : trois exemples. Exemple 2 : On dispose d un dé truqué. On sait que : p(1) = p(2) =1/6 ; p(3) = 1/3 p(4) = p(5) =1/12
 Probabilités. I - Rappel : trois exemples. Exemple 1 : Dans une classe de 25 élèves, il y a 16 filles. Tous les élèves sont blonds ou bruns. Parmi les filles, 6 sont blondes. Parmi les garçons, 3 sont
Probabilités. I - Rappel : trois exemples. Exemple 1 : Dans une classe de 25 élèves, il y a 16 filles. Tous les élèves sont blonds ou bruns. Parmi les filles, 6 sont blondes. Parmi les garçons, 3 sont
Continuité et dérivabilité d une fonction
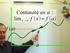 DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
DERNIÈRE IMPRESSIN LE 7 novembre 014 à 10:3 Continuité et dérivabilité d une fonction Table des matières 1 Continuité d une fonction 1.1 Limite finie en un point.......................... 1. Continuité
Section «Maturité fédérale» EXAMENS D'ADMISSION Session de février 2014 RÉCAPITULATIFS DES MATIÈRES EXAMINÉES. Formation visée
 EXAMENS D'ADMISSION Admission RÉCAPITULATIFS DES MATIÈRES EXAMINÉES MATIÈRES Préparation en 3 ou 4 semestres Formation visée Préparation complète en 1 an 2 ème partiel (semestriel) Niveau Durée de l examen
EXAMENS D'ADMISSION Admission RÉCAPITULATIFS DES MATIÈRES EXAMINÉES MATIÈRES Préparation en 3 ou 4 semestres Formation visée Préparation complète en 1 an 2 ème partiel (semestriel) Niveau Durée de l examen
Chapitre 5 : Flot maximal dans un graphe
 Graphes et RO TELECOM Nancy A Chapitre 5 : Flot maximal dans un graphe J.-F. Scheid 1 Plan du chapitre I. Définitions 1 Graphe Graphe valué 3 Représentation d un graphe (matrice d incidence, matrice d
Graphes et RO TELECOM Nancy A Chapitre 5 : Flot maximal dans un graphe J.-F. Scheid 1 Plan du chapitre I. Définitions 1 Graphe Graphe valué 3 Représentation d un graphe (matrice d incidence, matrice d
Cryptologie et physique quantique : Espoirs et menaces. Objectifs 2. distribué sous licence creative common détails sur www.matthieuamiguet.
 : Espoirs et menaces Matthieu Amiguet 2005 2006 Objectifs 2 Obtenir une compréhension de base des principes régissant le calcul quantique et la cryptographie quantique Comprendre les implications sur la
: Espoirs et menaces Matthieu Amiguet 2005 2006 Objectifs 2 Obtenir une compréhension de base des principes régissant le calcul quantique et la cryptographie quantique Comprendre les implications sur la
MÉTHODES NUMERIQUES. Cours. Licence de Physique Année Universitaire : 2010-2011 Licence Chimie, parcours Physique. Semestre S3
 Licence de Physique Année Universitaire : 2010-2011 Licence Chimie, parcours Physique Semestre S3 Cours MÉTHODES NUMERIQUES Chargé du Cours : M. GAGOU Yaovi E-mail :.gagou@u-picardie.fr URL : http://www.u-picardie.fr/gagou
Licence de Physique Année Universitaire : 2010-2011 Licence Chimie, parcours Physique Semestre S3 Cours MÉTHODES NUMERIQUES Chargé du Cours : M. GAGOU Yaovi E-mail :.gagou@u-picardie.fr URL : http://www.u-picardie.fr/gagou
L'instruction if permet d'exécuter des instructions différentes selon qu'une condition est vraie ou fausse. Sa forme de base est la suivante:
 420-183 Programmation 1 8. Les structures conditionnelles Dans l'écriture de tout programme informatique, une des premières nécessités que nous rencontrons est de pouvoir faire des choix. Dans une application
420-183 Programmation 1 8. Les structures conditionnelles Dans l'écriture de tout programme informatique, une des premières nécessités que nous rencontrons est de pouvoir faire des choix. Dans une application
